Ограниченные и неограниченные последовательности
Определение. Последовательность 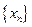 называется ограниченной, если существует такое число
называется ограниченной, если существует такое число 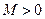 , что для любого
, что для любого 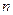 справедливо неравенство:
справедливо неравенство:
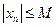
т.е. все члены последовательности принадлежат отрезку 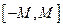 .
.
Определение. Последовательность 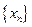 называется ограниченной сверху, если для любого
называется ограниченной сверху, если для любого 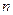 существует такое число
существует такое число 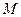 , что
, что
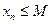 .
.
Определение. Последовательность 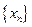 называется ограниченной снизу, если для любого n существует такое число
называется ограниченной снизу, если для любого n существует такое число 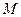 , что
, что
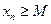
Пример. 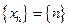 – ограничена снизу {1, 2, 3, … }.
– ограничена снизу {1, 2, 3, … }.
Определение. Число 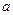 называется пределом последовательности
называется пределом последовательности 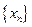 , если для любого положительного
, если для любого положительного 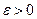 существует такой номер
существует такой номер 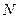 , что для всех
, что для всех 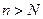 выполняется неравенство:
выполняется неравенство:
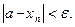
Обозначение: 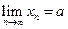 . В этом случае говорят, что последовательность
. В этом случае говорят, что последовательность 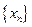 сходится к
сходится к 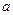 при
при 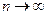 .
.
Пример. Доказать, что предел последовательности 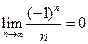 .
.
Пусть при 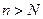 верно
верно 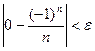 , т.е.
, т.е.  . Это верно при
. Это верно при 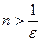 , таким образом, если за
, таким образом, если за 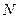 взять целую часть от
взять целую часть от 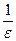 , то утверждение, приведенное выше, выполняется.
, то утверждение, приведенное выше, выполняется.
Пример. Показать, что при 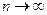 последовательность
последовательность 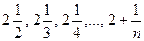 имеет пределом число 2. Имеем
имеет пределом число 2. Имеем 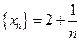 ;
; 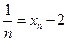 .Для любого положительного числа
.Для любого положительного числа 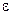 существует такое натуральное число
существует такое натуральное число 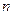 , что
, что 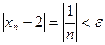 , т.е.
, т.е.  .
.
Теорема. Последовательность не может иметь более одного предела.
Доказательство. Предположим, что последовательность 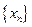 имеет два предела
имеет два предела 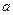 и
и 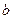 , не равные друг другу.
, не равные друг другу.
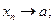
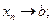
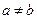 .
.
Тогда по определению существует такое число 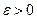 , что
, что
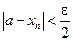 и
и 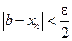 .
.
Запишем выражение: 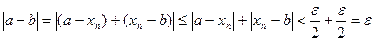 .
.
Так как 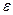 - любоеположительноечисло, то
- любоеположительноечисло, то 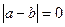 , т.е.
, т.е. 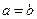 . Теорема доказана.
. Теорема доказана.
Теорема. Если 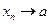 , то
, то 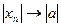 .
.
Доказательство. Из 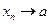 следует, что
следует, что 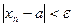 . В то же время:
. В то же время:
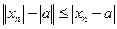 , т.е.
, т.е. 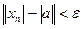 , т.е.
, т.е. 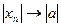 . Теорема доказана.
. Теорема доказана.
Теорема. Если 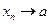 , то последовательность
, то последовательность 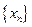 ограничена.
ограничена.
Необходимо отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость.
Например, последовательность 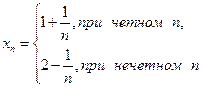 не имеет предел. В то же время
не имеет предел. В то же время 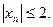
Дата добавления: 2015-11-28; просмотров: 1081;
