Монотонные последовательности
Определении
1) Если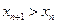 
для всех 
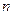, то последовательность называется возрастающей.
2) Если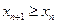 
для всех 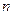, то последовательность называется неубывающей.
3) Если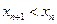 
для всех 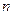, то последовательность называется убывающей.
4) Если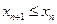 
для всех 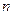, то последовательность называется невозрастающей.
Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными.
Пример.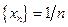 
– убывающая и ограниченная; 
– возрастающая и неограниченная.
Пример. Доказать, что последовательность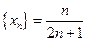 
монотонная и возрастающая.
Найдем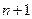 
-й член последовательности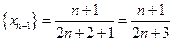 
Найдем знак разности: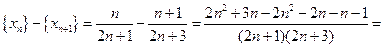 
, т.к.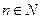 
, то знаменатель положительный при любом .
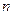Таким образом, 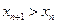. Последовательность возрастающая, что и следовало доказать.
Пример. Выяснить является возрастающей или убывающей последовательность
.
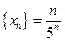Найдём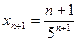 
. Определим разность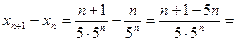 
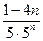, так как 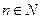, то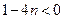 
, т.е. 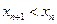. Последовательность монотонно убывает.
Заметим, что монотонные последовательности являютс ограниченными по крайней мере с одной стороны.
Теорема. Монотонная ограниченная последовательность имеет конечный предел.
Доказательство. Рассмотрим монотонную неубывающую последовательность
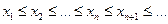
Эта последовательность ограничена сверху: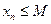 
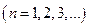, где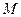 
– некоторое число. Так как любое ограниченное сверху, числовое множество имеет точную верхнюю грань, то для любого 
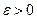существует число 
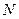такое, что 
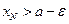, где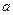 
– точная верхняя грань множества значений последовательности.
Так как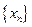 
- неубывающая последовательность, то при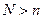 
,
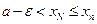. Отсюда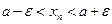 
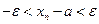или 
или 
, т.е.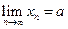 
.
Для остальных монотонных последовательностей доказательство аналогично. Теорема доказана.
Число е
Рассмотрим последовательность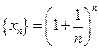 
.Если последовательность 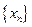монотонная и ограниченная, то она имеет конечный предел. По формуле бинома Ньютона:
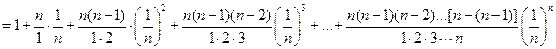
или
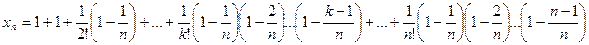
Покажем, что последовательность 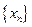– возрастающая. Действительно, запишем выражение 
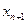и сравним его с выражением 
:
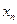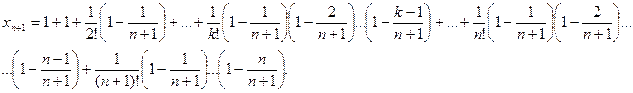Каждое слагаемое в выражении 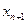больше соответствующего значения 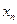, и, кроме того, у последовательности 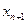добавляется еще одно положительное слагаемое. Таким образом, для любого натурального числа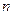 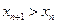, т.е последовательность 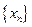возрастающая.
Докажем теперь, что при любом n ее члены не превосходят трех: 
.
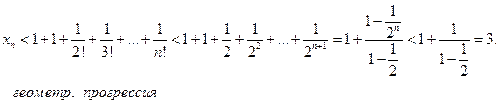
Таким образом, последовательность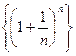 
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
.
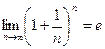Число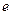 
является трпансцендентным числом и приблизительно равно
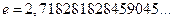
Число 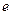является основанием натурального логарифма.
Дата добавления: 2015-11-28; просмотров: 866;