Дифференциальное уравнение затухающих колебаний и его решение

В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой F_y в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: F_тр = 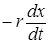. Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:

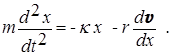(8)

Разделив левую и правую части уравнения (8) на m , обозначив r/m = 2b и сохранив обозначение к/m = w₀² , приведем это уравнение к виду:

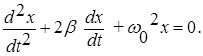(9)

Решение этого уравнения имеет вид:

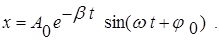(10)

Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы b и w. Коэффициент b = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания b. По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний. Это уменьшение зависит от коэффициента затухания. Оказывается, что

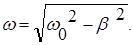(11)

Колебательный процесс может происходить лишь при условии:
(w₀² - b ²)>0, когда частота w в формуле (11) является действительной величиной . Если же затухание в системе слишком велико (w₀ < b ) , то под корнем в формуле (11) оказывается отрицательная величина, - в этом случае движение не имеет периодического характера.

Графически затухающее колебания представлено на рис.2, где сплошной линией показана зависимость смещения от времени, а пунктирной - экспоненциальный закон убывания амплитуды.