Дифференциальное уравнение гармонических колебаний и его решение

Гармонические колебания

Простейшим видом колебательного движения являются гармонические колебания, когда колеблющаяся величина изменяется со временем по закону синуса или косинуса.

Дифференциальное уравнение гармонических колебаний и его решение

Покажем, что гармоническое колебание возникает под действием упругой силы.

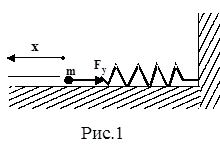
Представим материальную точку массой m, закрепленную на пружине жесткости ки расположенную на абсолютно гладкой горизонтальной поверхности (см. рис. 1). Если растянуть пружину на расстояние х, то со стороны пружины на эту точку действует упругая сила F_y , пропорциональная смещению х по закону Гука:

F_y = - кх.

Знак “минус” указывает на противоположность направлений смещения и действия силы упругости.

Чтобы установить характер движения, т.е. зависимость
х = f(t), запишем для этого случая дифференциальное уравнение, считая что в рассматриваемой системе движение определяется только наличием силы упругости:

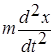= - кх. (1)

Разделим левую и правую части уравнения (1) на mи обозначим отношение положительных величин к и m через w₀² :

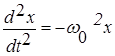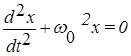или . (2)

Решение дифференциального уравнения (2) имеет вид:

х = А₀ sin (w₀ t + j₀ ) (3)

и показывает, что при наличии в системе лишь силы упругости движение совершается по гармоническому закону. Величина 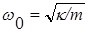, представляет собой циклическую частоту колебаний, А₀ - амплитуду, j₀ - начальную фазу, (w₀ t + j ) - фазу колебаний. Период колебаний 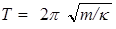, а частота
n = 1/ Т.

Зависимость скорости (v) движения материальной точки от времени при гармоническом колебании найдем, взяв производную по времени от формулы (3):

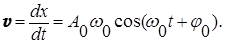(4)

Из сравнения выражений (3) и (4) видно, что смещение и скорость гармонического колебания различаются по фазе на p /2: скорость максимальна при прохождении точкой положения равновесия (смещение равно нулю), наоборот, при максимальном смещении (равном амплитуде) скорость равна нулю.

Выражение для ускорения получается дифференцированием формулы (4):

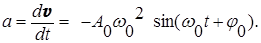(5)

Из формулы (3) следует, что смещение и ускорение изменяются в противофазе.