Разложение колебаний в ряд Фурье. Гармонический спектр сложных колебаний

Рассмотрение рис.4 приводит к утверждению, обратному сказанному выше и известному как теорема Фурье: любое сложное периодическое движение x(t) = x(t +T) c периодом Т можно представить в виде суммы простых составляющих гармонических колебаний (гармоник). Частоты этих гармоник кратны основной частоте w рассматриваемого периодического процесса.

Первая гармоника имеет частоту w = 2p /Т , вторая - 2w , третья - 3w и т.д.

Это утверждение можно записать в виде формулы, представляющей ряд Фурье:

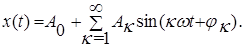(22)

Здесь А_к - амплитуды складываемых гармоник, а j_к - их начальные фазы. Первая гармоника, имеющая частоту w , обладает амплитудой А₁ , и начальной фазой j₁ , вторая (с частотой 2w ) имеет амплитуду А₂ и начальную фазу j₂ и т.д.

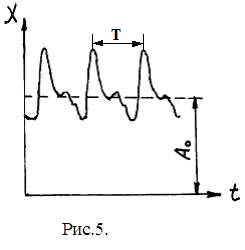
Слагаемое А₀ в формуле (22) представляет собой постоянную величину, имеющую смысл постоянной составляющей сложного периодического процесса. На рис.5 представлена периодическая функция х(t), описывающая процессы, где колебания некоторой величины (например, пульсовые изменения кровенаполнения сосуда) происходят на фоне ее среднего постоянного значения (например, среднего уровня кровенаполнения), которое и характеризуется величиной А₀ в формуле (22) .

В записанной для общего случая формуле (22) число гармоник, входящих в состав сложного колебания , представляется бесконечно большим. При рассмотрении реальных колебательных процессов следует учесть, что вклад отдельных гармонических составляющих в анализируемое сложное колебание различен - в формулу (22) отдельные гармоники входят с разными амплитудами.

График, на котором по оси абсцисс отложены частоты гармоник, а по оси ординат - соответствующие им амплитуды, представляет собой гармонический спектр сложного колебания(см. рис.6).

Из рассмотрения рис. 6 можно сделать вывод, что гармоники, частота которых превышает w ₁₀ , имеют малую амплитуды и, следовательно, их вклад в колебание, гармонический спектр которого представлен на рисунке, незначителен. Поэтому ряд Фурье для этого случая можно считать состоит из 10 слагаемых ( к = 1,2,3,.....,10 ), а вся информация о сложном колебательном процессе заключена в полосе частот от w₁ (основная частота процесса) до w₁₀ .