Класифікація в’язей і їхні рівняння

Предмет аналітичної механіки

Аналітична механіка є сукупність найбільш загальних аналітичних методів розв’язання задач механіки. Вона встановлює загальні, єдині методи вивчення руху і рівноваги стосовно до всіх матеріальних тіл. Такі методи являють собою дослідження засобами математичного аналізу всіх можливих рухів матеріальної системи. При цьому виводяться рівняння руху однієї і тієї ж структури, незалежної від вигляду системи і характера умов, що накладено на рух системи.

Загальні рівняння аналітичної механіки виявляються більш зручними що до розв’язання конкретних задач механіки, так і до загальних досліджень властивостей руху.

Всі теореми і рівняння аналітичної механіки випливають з деяких основних понять і припущень.

Засновником аналітичної механіки є видатний французький вчений математик і механік Жозеф Луі Лагранж. Механіка Лагранжа (на відміну від механіки Ньютона, яка досліджує рух лише вільних точок і систем) вивчає рух і рівновагу невільних (зв’язаних) механічних систем.

Зв’язаною матеріальною системоюназивається система, на рух якої накладено якісь обмеження геометричного або кінематичного характеру.

Тіла, котрі обмежують свободу руху розглядуваного тіла, називаються в’язями.Сили, з якими в’язі діють на матеріальну систему, що рухається, називаються динамічними реакціями в’язей.

Тут ми будемо вивчати рух зв’язаної матеріальної системи, яка під дією прикладених до неї сил не може (через накладені на неї в’язі) рухатися довільно із довільною швидкістю. Рух такої системи залежить не тільки від сил, що діють на неї, а й від накладених на її точки в’язей. При цьому значення початкових умов не можуть бути незалежними одне від одного, а мусять задовольняти певні рівняння в’язей.

Класифікація в’язей і їхні рівняння

За характером дії в’язей на матеріальну систему їх можна поділити: на стаціонарні і нестаціонарні, на голономні і неголономні, на утримуючі і неутримуючі.

В’язі, рівняння яких не залежить від часу 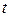в явному вигляді, називаються стаціонарними або склероном ними.

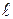Прикладом стаціонарної в’язі може бути абсолютно жорсткий стержень довжиною , що з’єднує рухому точку 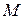з нерухомим сферичним шарніром .

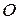Ця в’язь припускає рух точки М по поверхні сфери радіусом 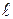(рис. 11.1). Рівняння стаціонарної в’язі має вигляд:

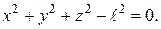(11.1)

Якщо рівняння в’язей залежить від часу 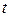в явному вигляді, вони називаються нестаціонарними або реономними.

Прикладом такої в’язі може бути в’язь у вигляді гнучкої нерозтяжної і невагомої нитки 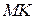довжиною 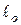, що проходить через кільце 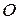(рис. 11.2). До одного кінця нитки прикріплено матеріальну точку 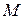, а інший вільний кінець нитки 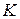переміщується зі сталою швидкістю 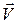. З плином часу довжина правої частини нитки буде зменшуватися згідно до рівняння: .

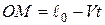Рівняння такої нестаціонарної в’язі в цьому випадку матиме вигляд:

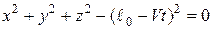. (11.2)

Якщо в’язі, що накладені на матеріальну точку, обмежують лише свободу переміщення точки в просторі, не накладаючи обмежень на швидкість її руху, такі в’язі називаються голономними або геометричними.

Рівняння голономної в’язі має такий вигляд:

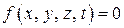. (11.3)

В’язі, що обмежують не тільки координати точки, але й її швидкість, називаються неголономними або кінематичними.

Рівняння неголономної в’язі має вигляд:

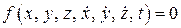. (11.4)

Неутримуючою або однобічною називається в’язь, що перешкоджає руху точки в якому-небудь одному напряму і припускає в зворотньому.

Прикладом однобічної в’язі може бути горизонтальна площина (рис. 11.3, а).

Неутримуючою або двобічною називається в’язь, що перешкоджає переміщенню тіла в двох протилежних напрямах (рис. 11.3, б).