Можливі або віртуальні переміщення механічної системи
Уявлення про можливі переміщення є одним з фундаментальних в аналітичній механіці.
Найкраще це поняття можна проілюструвати на прикладі стаціонарної в’язі, накладеної на матеріальну точку.
Розглянемо в’язь у вигляді нерухомої поверхні.
 Розглядаючи в якийсь момент часу розташування точки на поверхні, уявимо собі, які елементарні (доволі малі) переміщення припускає ця в’язь. Такі переміщення
Розглядаючи в якийсь момент часу розташування точки на поверхні, уявимо собі, які елементарні (доволі малі) переміщення припускає ця в’язь. Такі переміщення 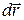 зображуються прирістами радіуса – вектора
зображуються прирістами радіуса – вектора 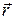 точки
точки 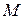 , що розташовані у вигляді віяла на поверхні (рис. 11.4).
, що розташовані у вигляді віяла на поверхні (рис. 11.4).
З точністю до нескінченно малих величин вищого порядку ці прирости 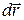 можна зобразити векторами
можна зобразити векторами 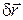 , розташованими в площині, дотичній до поверхні в даній точці.
, розташованими в площині, дотичній до поверхні в даній точці.
Треба відрізняти дійсні переміщення від можливих.
Серед усіх кінематично можливих переміщень здійснюється лише одне, тільки те, котре обумовлене діючими силами.
Дійсним переміщенням точки називається таке елементарне переміщення, яке фактично відбувається в просторі за час 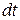 при накладених в’язях під дією прикладених активних сил.
при накладених в’язях під дією прикладених активних сил.
Надалі будемо позначати дійсні переміщення 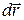 , а можливі –
, а можливі – 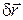 , які є варіаціями радіуса – вектора точки.
, які є варіаціями радіуса – вектора точки.
Вектор 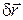 спрямований по дотичній до траєкторії переміщення точки і являє собою головну лінійну частину вектора
спрямований по дотичній до траєкторії переміщення точки і являє собою головну лінійну частину вектора 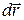 . Різниця між вектором
. Різниця між вектором 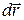 і вектором
і вектором 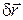 є вектор більш високого порядку малості, ніж вектор
є вектор більш високого порядку малості, ніж вектор 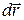 .
.
 Наприклад, можливим переміщенням важіля
Наприклад, можливим переміщенням важіля 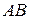 є його поворот на нескінченно малий кут
є його поворот на нескінченно малий кут 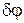 навколо точки
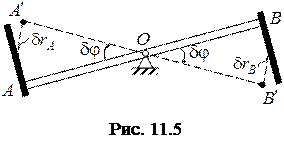
навколо точки 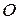 (рис. 11.5). При цьому повертанні точки
(рис. 11.5). При цьому повертанні точки 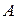 і
і 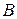 мають переміститися за дугами відповідного кола в положення
мають переміститися за дугами відповідного кола в положення 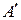 і
і 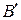 . Можливими переміщеннями точок
. Можливими переміщеннями точок 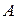 і
і 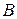 будуть переміщення
будуть переміщення 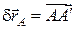 і
і 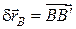 у вигляді прямолінійних відрізків, відкладених вздовж дотичних до траєкторій цих точок. За модулем ці переміщення дорівнюють:
у вигляді прямолінійних відрізків, відкладених вздовж дотичних до траєкторій цих точок. За модулем ці переміщення дорівнюють:
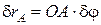 та
та 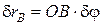 .
.
Отже, криволінійні переміщення точок замінюються прямолінійними відрізками, відкладеними вздовж дотичних до траєкторій точок.
Таким чином, можливим або віртуальним перемщенням точки називають уявне нескінченно мале переміщення точки, допустиме накладеними на неї в’язями, в даний момент часу.
Якщо в’язь, накладена на точку, стаціонарна, кожне дійсне переміщення збігається з одним з можливих переміщень.
Для відшукання можливих переміщень у випадку нестаціонарної в’язі останню необхідно перетворити в стаціонарну, «зупинивши» час 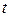 . Можливі переміщення в такому випадку визначаються при фіксованому для даного положення часу
. Можливі переміщення в такому випадку визначаються при фіксованому для даного положення часу 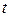 . Дійсне переміщення
. Дійсне переміщення 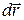 у випадку нестаціонарної в’язі визначається як сума відносного переміщення
у випадку нестаціонарної в’язі визначається як сума відносного переміщення 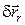 і переносного переміщення
і переносного переміщення 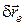 , що відбувається внаслідок руху в’язі разом з матеріальною точкою. В такому випадку дійсне переміщення може не збігатися з жодним із можливих переміщень.
, що відбувається внаслідок руху в’язі разом з матеріальною точкою. В такому випадку дійсне переміщення може не збігатися з жодним із можливих переміщень.
Ідеальні в’язі
Звільнюючи механічну систему від в’язей і замінюючи їхні дії на цю систему реакціями 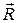 , ми формально невільну (зв’язану) механічну систему розглядаємо як вільну. Такий прийом дозволяє лише записати для кожної точки системи рівняння руху, які містять невідомі значення реакцій. Проте в більшості випадків відомості про реакції в’язей не потрібні.
, ми формально невільну (зв’язану) механічну систему розглядаємо як вільну. Такий прийом дозволяє лише записати для кожної точки системи рівняння руху, які містять невідомі значення реакцій. Проте в більшості випадків відомості про реакції в’язей не потрібні.
Лагранж запропонував метод розв’язання задач динаміки зв’язаної системи, в якому реакції в’язей автоматично вилучаються з розгляду. Цей метод грунтується на важливій властивості більшості в’язей, яка полягає в тому, що сума робіт реакцій цих в’язей на будь-якому можливому переміщенні дорівнює нулю.
В’язі, сума робіт яких на будь-якому можливому переміщенні дорівнює нулю, називаються ідеальним, тобто для ідеальних в’язей виконується умова:
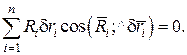 (11.5)
(11.5)

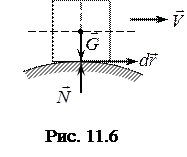 Приклад 1. Розглянемо ковзання тіла по ідеально гладенькій поверхні (рис. 11.6). Надамо системі можливе переміщення
Приклад 1. Розглянемо ковзання тіла по ідеально гладенькій поверхні (рис. 11.6). Надамо системі можливе переміщення 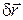 і обчислимо роботу реакцій в’язей на цьому переміщенні. Оскільки на тіло діє лише нормальна реакція
і обчислимо роботу реакцій в’язей на цьому переміщенні. Оскільки на тіло діє лише нормальна реакція 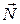 , то її робота дорівнюватиме:
, то її робота дорівнюватиме:
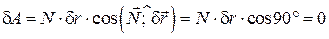 .
.
Приклад 2.Нехай колесо котиться без ковзання по шорсткій поверхні (рис. 11.7). Точкастикання колеса і в’язі (т. Р) буде миттєвим центром швидкості тіла 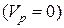 і її можливе переміщення дорівнюватиме нулю. Оскільки до цієї точки прикладено реакції
і її можливе переміщення дорівнюватиме нулю. Оскільки до цієї точки прикладено реакції 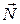 і
і 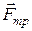 , то робота цих реакцій на нульовому переміщенні також дорівнює нулю.
, то робота цих реакцій на нульовому переміщенні також дорівнює нулю.
Дата добавления: 2015-11-28; просмотров: 2171;
