Функціональне моделювання за допомогою програми МАЕС-П
Необхідно відзначити, що об'єкти різної фізичної природи описуються системами ЗДР. Це механічні, гідравлічні, теплові системи. Існує аналогія між цими системами, наприклад, аналогами електричної напруги є тиск, температура, швидкість; електричного струму – сили і потоки рідини, газу, теплоти. Існують і аналоги закону Кирхгофа I і II. Так, для механічної поступальної системи – принцип Даламбера: сума сил, що діють на тіло, дорівнює нулю 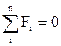 - аналогічно
- аналогічно 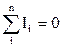 , а сума швидкостей, що діють на тіло, дорівнює нулю
, а сума швидкостей, що діють на тіло, дорівнює нулю 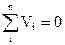 - аналогічно
- аналогічно 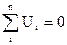 і т.д.
і т.д.
Це свідчить про те, що методи і програми аналізу електричних схем можуть бути з успіхом застосовані для аналізу систем і іншої фізичної
природи, особливо на функціональному рівні.
Характерним прикладом задач, для функціонального моделювання яких з успіхом можна використовувати програми АСхП, зокрема, програму МАЕС-П, є дослідження поведінки систем автоматичного регулювання САР або АСУТП, функціональні схеми яких складаються з типових ланок: диференцюючих, інтегруючих, нелінійних, підсумовуючих і т.д.
Розглянемо більш докладно функціональне моделювання САР. Будь який блок (ланку) САР у МАЕС-П можна представити моделлю у виді відповідного набору керованих джерел струму, опорів і ємностей, які показують залежність між вихідними і вхідними сигналами цих блоків. Розглянемо побудову електричних моделей деяких функціональних блоків.
Підсилюючий блок. Рівняння цього блоку y(t)=kx(t).
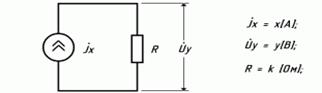 Рисунок 5.15-Еквівалентна електрична схема підсилюючого блоку
Рисунок 5.15-Еквівалентна електрична схема підсилюючого блоку
Якщо уявити, що джерело струму вищенаведеної схеми Jx відображає вхідний сигнал x з масштабом Mx=(Ix/x)=1, а напруга на резисторі R - вихідний сигнал y з масштабом My=Uy/y, то з рівняння кола Uy= Ix*R одержуємо My*y=R*Mx*x або y=(Mx/My)*R*x=R*x .
Порівнявши ці рівняння кола і підсилюючого блоку, одержимо R=k. Вхідні і вихідні сигнали електричної моделі і блоку будуть чисельно збігатися.
Аналогічно одержуємо еквівалентну електричну схему підсумовуючої ланки, рівняння якої y=k 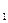 *x
*x 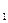 +k
+k 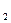 *x
*x  +…+kn*xn.
+…+kn*xn.
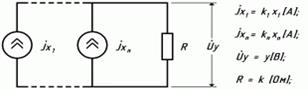
Рисунок 5.16-Еквівалентна електрична схема підсумовуючого блоку
Інтегруючий блокможе бути представлений такою еквівалентною схемою
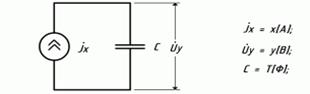
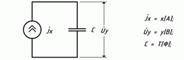
Рисунок 5.17-Еквівалентна електрична схема інтегруючогоблоку
Рівняння блоку 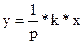 .Рівняння кола
.Рівняння кола 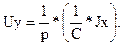
Виразивши Uy і Ixчерез yі x,одержимо
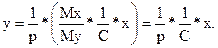
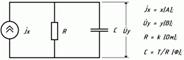
Звідки Jx=x [A], Uy=y [B]. C=1/k .
Аналогічно одержимо еквівалентну електричну схему аперіодичної ланки.
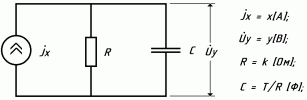
Рисунок 5.18-Еквівалентна електрична схема аперіодичногоблоку
Рівняння ланки 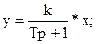
рівняння кола 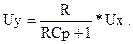
ЯкщоJx=x [A], а Uy=y [B], то R=k [Ом]; C=T/R [Ф].
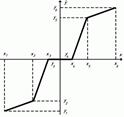
Нелінійний блок: y=f(x)=ТАБ(x)може бути представлений залежним джерелом струму Jy=f(Ux)=ТАБ(x); Jy=y [A]; Ux=x [B]
.
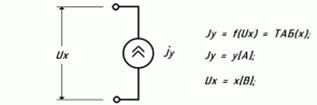
Рисунок 5.19-Еквівалентна електрична схема нелінійногоблоку
Зведемо отримані результати в таблицю 5.1 за умови, що mx = my =1.
Розглянемо функціональну модель типової САР на прикладі САР палива паронагріваючого котла АСУ ТП ТЕЦ ( рис. 5.20). Ця САР підтримує тиск пари в барабані котла на заданому рівні, регулюючи подачу палива. Вона складається з виконавчого органа, об'єкта регулювання (казана), датчика тиску пари в барабані казана і регулятора.
Таблиця 5.1.Еквівалентні електричні схеми типових блоків САР
| Тип блоку | Рівняння блоку | Еквівалентна електрична схема |
| Підсилю-ючий | 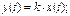
|
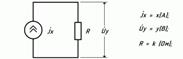
|
| Склада-ючий | 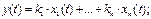
|
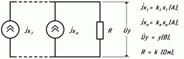
|
| Інтегру-ючий | 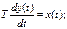
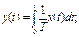 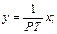
| 
|
| Аперіо- дичний | 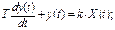
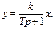
| 
|
| Неліній- Ний |
|
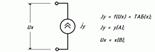 ЭЛЕМЕНТЫ:
JY,0-1 = FЗ(0,0,ТАБX#U1);
ТАБЛИЦЫ:
ТАБX = x1 ,y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6;
ЭЛЕМЕНТЫ:
JY,0-1 = FЗ(0,0,ТАБX#U1);
ТАБЛИЦЫ:
ТАБX = x1 ,y1, x2, y2, x3, y3, x4, y4, x5, y5, x6, y6;
|
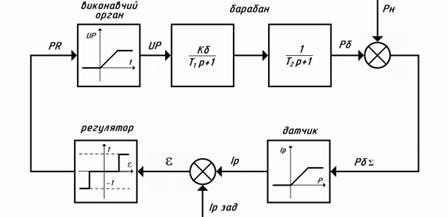
Рисунок 5.20- Функціональна схема типової САР
На еквівалентній електричній схемі САР (рис. 5.21) нелінійне джерело J1 моделює нелінійну характеристику регулятора. Виконавчий механізм моделюється елементами С1 і JK; казан – елементами J2, R2,С2 і J3, R3,С3, навантаження - Jн; сумарний тиск - UR4, датчик - нелінійним джерелом J5; задане значення тиску - джерелом J6, а помилка 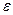 - напругою на опорі R5.
- напругою на опорі R5.
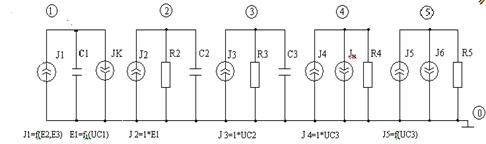
Рисунок 5.21- Еквівалентна електрична схема функціональної моделі типової САР
Дата добавления: 2015-11-28; просмотров: 991;
