Основные свойства жидкости
Основные свойства жидкости и газа. Гидростатика
Основные свойства жидкости
Система материальных точек, непрерывно заполняющая некоторую часть пространства, называется сплошной средой. Сплошная среда представляет собой модель реально существующих материалов, т.е. является определенной идеализацией, полезной для решения многих практических задач. Моделью сплошной среды пользуются для описания жидких тел (воды, нефти, нефтепродуктов и т.д.), твердых деформируемых тел (металлов, горных пород), а также газообразных веществ (воздуха, природного газа). Жидкость в гидромеханике рассматривается как сплошная среда, что очень удобно при использовании математического аппарата непрерывных функций.
Плотность характеризует массу сплошной среды (в том числе и жидкости), содержащуюся в единице объема.
Средняя плотность среды в достаточно малом объеме DV, содержащем точку М(х, у, z), определяется по формуле
rср = Dm/DV,  (1.1)
(1.1)
где D m — масса сплошной среды, заключенная в объеме DV.
В точке М плотность равна
r (х, у, z, t) = 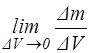 . (1.1¢)
. (1.1¢)
Если r не зависит от координат х, у, z, т.е. плотность одна и та же во всех точках среды, то последняя называется однородной.
Наряду с плотностью среды вводится ее удельный вес
g = rg, (1.2)
где g — ускорение свободного падения.
Размерности и единицы измерения для величин r и g приведены ниже.
Величина ………………………. Плотность Удельный вес
Размерность …………………. M/L3 M/(L2T2)
Единица измерения в СИ …….. кг/м3 кг/(м2× с2) или Н/м2
Силы, действующие на частицы сплошной среды, делятся на два вида: массовые и поверхностные.
Силы, распределенные по объему V, называются массовыми силами. Примером таких сил может служить сила тяжести, сила инерции, электромагнитные силы.
Массовые силы характеризуются плотностью массовых сил (напряжением массовых сил). Если Dm — масса элементарного объема DV, содержащего точку М(х, у, z), а D 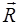 — сила, действующая со стороны внешних тел на частицы, входящие в объем DV, то плотность массовых сил
— сила, действующая со стороны внешних тел на частицы, входящие в объем DV, то плотность массовых сил 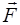 точке М(х, у, z) определяется из выражения
точке М(х, у, z) определяется из выражения
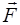 (x,y,z,) =
(x,y,z,) = 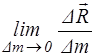 . (1.3.)
. (1.3.)
Плотность массовых сил 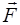 — векторная величина и имеет размерность ускорения
— векторная величина и имеет размерность ускорения
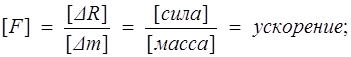
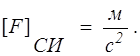
Поверхностные силы представляют собой силы, распределенные по поверхности, ограничивающей рассматриваемый объем. На внешней поверхности тела поверхностные силы отражают взаимодействие тела с окружающей средой. К поверхностным силам относят силы давления, силы реакции тела на поток, силы внутреннего трения в среде.
Поверхностные силы в сплошной среде характеризуются вектором напряжений
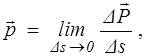 (1.4)
(1.4)
где D 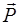 — главный вектор сил, приложенных с одной стороны к некоторой малой площадке Ds.
— главный вектор сил, приложенных с одной стороны к некоторой малой площадке Ds.
Напряжение — размерная величина. Размерность напряжения определяется на основе формулы (1.4) :
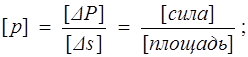
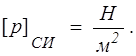
В каждой точке М (х, у, z) сплошной среды можно построить бесконечное число векторов напряжений, определяемых ориентацией выбранной площадки. Каждый из этих векторов может иметь нормальную по отношению к площадке и касательную составляющие.
В покоящейся жидкости отсутствуют касательные напряжения, а нормальные напряжения являются сжимающими. Растяжения в среде, называемой жидкостью, невозможны, а бесконечно малые сдвигающие усилия сразу же вызывают начало течения. Поэтому жидкость принимает форму того сосуда, в который она налита.
Основной характерный параметр для жидкости — давление р. В покоящейся жидкости модули нормальных напряжений на всех площадках, проходящих через данную точку, равны между собой и называются давлением в данной точке.
Давление — это скалярная величина, имеющая размерность напряжения
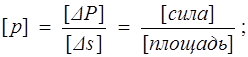
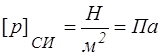 .
.
Различают давление абсолютное, избыточное и вакуум. Давление р, определенное выше, называют абсолютным. Если за начало отсчета принимается атмосферное давление ра , то избыток абсолютного давления р над атмосферным называется избыточным давлением pи= р — ра. При этом может быть два случая:
1) абсолютное давление р больше ра, тогда Ри= р — ра > 0 и измеряется манометрами, поэтому оно называется еще манометрическим;
2) абсолютное давление р меньше ра, тогда ри =р — ра < 0, и взятая с обратным знаком эта разность определяет вакуум: Рв = — р — = ра — р. Вакуум показывает, насколько абсолютное давление меньше атмосферного. Величина рвизмеряется вакуумметрами.
Пар называется насыщенным, когда число молекул, переходящих из жидкости в пар, равно числу молекул, совершающих обратный переход. В этом случае в паре устанавливается вполне определенное при данной температуре давление, называемое давлением насыщенного пара рп.
Давление насыщенного пара рп зависит от рода жидкости и от температуры. Давления насыщенных паров воды, легкой нефти, бензина и глинистого раствора при разных температурах приведены в табл. 1.1.
Кипение в жидкости наступает, когда температура становится выше, чем температура кипения при данном давлении, или вследствие понижения давления до значений, меньших давления насыщенного пара при данной температуре. Кипение, возникающее в движущейся жидкости вследствие местных понижений давления до давления насыщенного пара, называется кавитацией.
Жидкость называется несжимаемой, если ее плотность не зависит от
давления, т.е. dr /dp = 0.
Если плотность жидкости изменяется в зависимости от давления, то величина
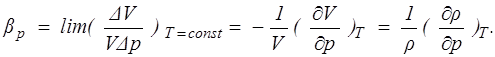 (1.5)
(1.5)
называется коэффициентом сжимаемости. Он равен относительному изменению объема жидкости при изменении давления на одну единицу. Коэффициент сжимаемости имеет размерность, обратную давлению:
[bp]СИ= Па-1 .
Таблица 1.1.
Давления насыщенных паров (Па) некоторых жидкостей
| Жидкость | Температура, °С | |||||
| Вода | ||||||
| Легкая нефть | — | — | — | |||
| Бензин | ||||||
| Глинистый раствор | — |
Продолжение табл. 1.1
| Жидкость | Температура, °С | ||||
| Вода | |||||
| Легкая нефть | — | — | — | ||
| Бензин | — | — | — | — | — |
| Глинистый раствор | — | — | — | — | — |
Величина обратная коэффициенту сжимаемости, называется модулем объемной упругости жидкости
К= 1/br . (1.6)
Для воды среднее значение модуля объемной упругости К=2 ×109 Па; Для керосина К=1,7 ×109 Па ; для дизельного топлива К=1,6 ×109 Па; для других нефтепродуктов К=1,3 ×109 Па.
Плотность жидкости может изменяться при изменении температуры. В этом случае изменение плотности характеризуется коэффициентом теплового объемного расширения bТ , определяемым по формуле
bТ = lim 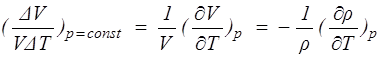 ,(1.7)
,(1.7)
Коэфициент теплового объемного расширения bТ равен относительному изменению объема жидкости при изменении температуры на один градус. Размерность bТ обратна температуре
[bТ] СИ = градус-1 .
Если известна плотность нефтепродуктов при 15 °С (r15) , то величину r при другой температуре можно определить по формуле Менделеева:
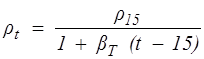 , (1.8)
, (1.8)
где t – температура нефтепродуктов, °С ; bТ – коэффициент, зависящий от r15 .
Значения коэффициента bТ в формуле Менделеева приведены ниже:
r15 , кг/м3 ……………… 700 800 850 900 920
bТ × 10 –4,°С ……………… 8,2 7,7 7,2 6,4 6,0
В общем случае
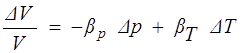 .
.
Идеальная и вязкая жидкости. Существуют две распространенные модели жидкости. Первая из них предполагает, что в жидкости и при движении нет касательных напряжений. Это модель идеальной жидкости. Вторая модель учитывает при движении касательные напряжения. Это модель вязкой жидкости.
В простейшем случае прямолинейного слоистого течения связь между касательным напряжениям t и производной скорости u по нормали определяется законом вязкого трения Ньютона
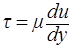 . (1.9)
. (1.9)
Коэффициент пропорциональности m в этой формуле называется динамическим коэффициентом вязкости. Этот коэффициент определяется свойствами жидкости и зависит от давления и температуры. Размерность динамического коэффициента вязкости
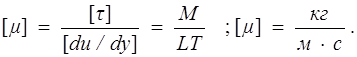
Для характеристики вязких жидкостей вводят еще один коэффициент – кинематический коэффициент вязкости v :
v=m /r
Дата добавления: 2016-01-20; просмотров: 913;
