Равномерное вращение сосуда вокруг вертикальной оси

В случае равномерного вращения цилиндрического сосуда вокруг вертикальной оси с угловой скоростью со (рис. 1.5) вектор напряже­ния массовых сил

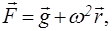(1.51)

а уравнение Эйлера (1.10) имеет вид

dp = r [w² ( xdx +ydy ) – gdz] = r (w ² rdr – gdz). (1.52)

Уравнение свободной поверхности (р = р₀ )

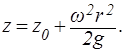(1.53)

Уравнение любой изобарической поверхности (р = const)

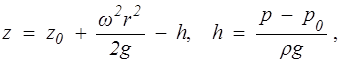(1.54)

где z₀ - координата точки пересечения свободной поверхности с осью вращения.

Изобарические поверхности - параболоиды вращения, ось которых совпадает с осью оz , а вершины смещены вдоль этой оси. Форма изоба­рических поверхностей не зависит от плотности жидкости.

Высота параболоида свободной поверхности (R - радиус сосуда)

H = w ²R²/2g. (1.55)

Координата z₀ его вершины определяется объемом жидкости в сосу­де. Если начальный уровень в сосуде h₀ , то

z₀ = h - 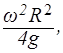(1.56)

откуда h₁ = h₀ –z₀ = H/2.

Закон распределения давления в жидкости

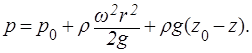(1.57)

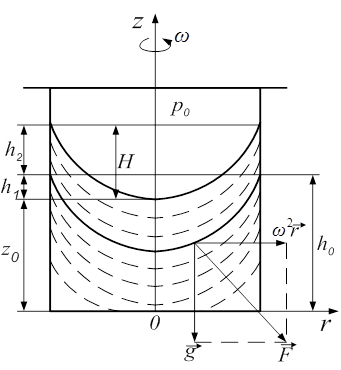
Рис. 1.5. Цилиндрический сосуд с жидкостью, вращающийся с постоян­ной угловой скоростью w

Изменение давления по вертикали (h — глубина точки под свобод­ной поверхностью) :

Р = Р₀ + r gh,

т.е. такое же, как в неподвижном сосуде.

Вопросы по теме 1.6.

1 . Какие силы действуют на жидкость при ее относительном покое?

2. Каковы форма изобарических поверхностей в жидкости и описы­вающее их уравнение при прямолинейном движении сосуда с постоян­ным ускорением?

3. Каковы форма изобарических поверхностей в жидкости и описы­вающее их уравнение при вращении сосуда с постоянной угловой ско­ростью и вертикальной осью вращения?

3. Каков закон распределения давления в жидкости по вертикали при ее относительном покое?

Основные понятия кинематики и динамики жидкости

Скорость частицы жидкости 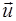зависит от координат х, у, z этой частицы и времени t, т.е.

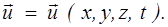
Плотность r и давление р также являются функциями координат и времени

r = r (x, y, z, t); p = p (x, у, z, t).

Если характеристики течения не зависят от времени, т.е. могут изме­няться лишь от точки к точке, то течение называется установившимся. Если в данной точке пространства характеристики течения изменяются со временем, то течение называется неустановившимся.

Линией тока называется линия, в каждой точке которой вектор скорости направлен по касательной к этой линии. Уравнения для линий тока имеют вид

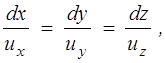(2.1)

где и_х, и_y , u_z — составляющие вектора скорости .

Совокупность линий тока, проходящих через замкнутый контур L, образует трубчатую поверхность — трубку тока. Жидкость, находя­щаяся внутри трубки тока, образует струйку. Если контур L мал, то трубка тока и струйка называются элементарными.

Сечение струйки s, нормальное в каждой своей точке к линиям то­ка, называется живым сечением.

Область пространства конечных размеров, занятая движущейся жидкостью, называется потоком. Поток обычно рассматривается как совокупность элементарных струек. Живое сечение потока определяется так же, как в случае элементарной струйки.

Гидравлический радиус R_г живого сечения определяется как отношение площади живого сечения s к смоченному периметру c, т.е.

R_г = s/c. (2.2)

Под смоченным периметром c понимается та часть геометри­ческого живого сечения, по которой жидкость соприкасается с твердыми стенками.

Если форма и площадь живого сечения по длине потока не изменяют­ся, то поток называется равномерным. В противном случае поток на­зывается неравномерным. В том случае, когда живое сечение плавно изменяется по длине, течение называется плавно изменяющимся.

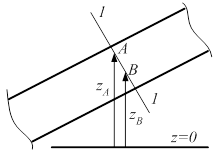
В живом сечении 1 — 1 (рис. 2.1) равномерного потока выполняется гидростатический закон распределения давления, т.е.

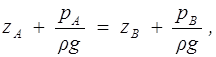(2.3)

где р_А, р_B — соответственно давления в произвольных точках А и В (с вертикальными координатами z_a, z_b) этого сечения; g — ускоре­ние свободного падения. В случае плавно изменяющегося течения ра­венство (2.3) выполняется приближенно.

Расходом жидкости через поверхность s называется количество жидкости, протекающей через эту поверхность _в единицу времени. Объемный расход Q, массовый расход Q_М > весовой расход q_G определяются по формулам

, (2.4)

где и_n — проекция скорости на нормаль к поверхности s.

Если s — живое сечение, то и_п = u. Для однородной жидкости

Q_m = rQ (2.5)

Рис. 2.1. Живое сечение равномерного потока

Средняя скорость u определяется из равенства

u=Q/s. (2.6)

Уравнение неразрывности для потока несжимаемой жидкости имеет вид

Q = u ₁ s₁ = u₂s₂, (2.7)

где u ₁ , u₂ — средние скорости в сечениях 1 - 1 и 2 - 2.

Уравнение Бернулли для элементарной струйки вязкой несжимае­мой жидкости при установившемся движении в поле силы тяжести имеет вид

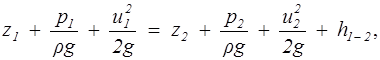(2.8)

где z₁, z₂ - расстояния от центров выбранных живых сечений 1 — 1 и 2 — 2 до некоторой произвольной горизонтальной плоскости z = 0 (рис. 2.2); u₁, u₂ - скорости; P₁,P₂ -давления в этих сечениях; h_1-2 — потери напора на участке между выбранными сечениями.

Уравнение Бернулли выражает собой закон сохранения механичес­кой энергии. Величина

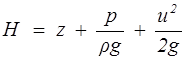(2.9)

называется полным напором и представляет собой удельную (прихо­дящуюся на единицу силы тяжести) механическую энергию жидкости в рассматриваемом сечении; z — геометрический напор или удельная потенциальная энергия положения; p/(rg) — пьезометрический напор или удельная потенциальная энергия давления; u²/(2g) - скоростной напор или удельная кинетическая энергия; h_1-2 — потери напора, т.е. часть удельной механической энергии, израсходованной на работу сил трения на участке между сечениями 1 — 1 и 2 — 2 (см. рис. 2.2).

В случае идеальной жидкости h_1-2 =0.

Для плавно изменяющегося потока при установившемся движении вязкой несжимаемой жидкости в поле силы тяжести уравнение Бернул­ли имеет вид

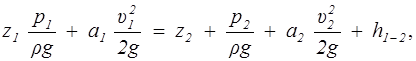(2.10)

где p₁, p₂ — давления в произвольно взятых точках сечений 1 — 1 и 2 — 2 скоординатами z₁ и z₂ соответственно (обычно берутся точки на оси потока); u ₁ , u₂ — средние скорости в этих сечениях; а₁ , а₂ — коэффи­циенты Кориолиса, учитывающие неравномерность распределения ско­ростей частиц жидкости в сечениях; при течении по круглой цилиндри­ческой трубке a = 2 для ламинарного режима течения и a » 1,1 — для турбулентного; при решении практических задач обычно принимается a = 1.

При использовании уравнения Бернулли (2.8) или (2.10) необходи­мо иметь в виду, что номера сечений возрастают в направлении течения жидкости. В качестве расчетных выбираются такие сечения (струйки) , в которых известны какие-либо из величин u ₁ , u₂ (u₁, u₂) и р₁, р₂ .

Плоскость z = 0 бывает удобно располагать таким образом, чтобы центр одного из выбранных сечений потока лежал в этой плоскости.

Потери напора h_1-2 , отнесенные к единице длины трубопровода, называются гидравлическим уклоном:

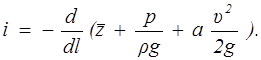(2.11)

В случае равномерного движения несжимаемой жидкости

i = h_l-2 / l, (2.12)

где l — расстояние между выбранными сечениями.

При движении жидкости по трубопроводу различают два вида потерь напора: потери по длине трубопровода h_д и потери в местных сопротив­лениях h_м . К потерям по длине относят потери на прямолинейных участ­ках трубопровода, а к потерям на местных сопротивлениях — потери на таких участках трубопровода, где нарушается нормальная конфигурация потока (внезапное расширение, поворот, запорная арматура и т.д.) .

Вопросы по теме 2.

1. Что называется линией тока?

2. Может ли жидкость протекать сквозь боковую поверхность труб­ки тока?

3. Что называется живым сечением потока?

4. Чем отличается уравнение Бернулли для струйки тока от уравне­ния Бернулли для потока?

5. Что такое гидравлический уклон?

6. Как определяется средняя скорость потока?

7. Какая связь между объемным, массовым и весовым расходами?

8. Как изменяются по длине неравномерного потока несжимаемой жидкости расход и средняя скорость?