Гидравлические сопротивления. Запас механической энергии жидкости, которым обладает каждая ее единица силы тяжести, называется напором Н

Запас механической энергии жидкости, которым обладает каждая ее единица силы тяжести, называется напором Н. Из-за работы сил трения напор по ходу движения жидкости непрерывно уменьшается. Разность начального и конечного напоров между двумя какими-либо живыми сечениями потока называется потерями напора h_пот . Эти потери напора представляют собой сумму потерь напора на трение по длине потока h_д и в местных сопротивлениях h_м

H_пот =h_д+h_м. (5.1)

Потери напора по длине для труб постоянного диаметра определяют­ся по формуле Дарси-Вейсбаха

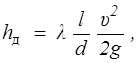(5.2)

где l — коэффициент гидравлического сопротивления (гидрав­лического трения); l — длина трубы; d —ее внутренний диаметр; u —средняя скорость потока.

В общем случае l является функцией числа Рейнольдса (Re) и относительной шероховатости стенок трубы D/d. Здесь D —абсолютная эквивалентная шероховатость, т.е. такая высота равномерно-зернистой шероховатости, при которой в квадратичной зоне сопротивления потери напора равны потерям напора для данной естест­венной шероховатости трубы (примерные значения D — приведены в прил. 1).

Итак, в общем виде l = l (Re, D/d). Численно l определяется в зависимости от области сопротивления. При ламинарном режиме движения (Re < Re_кр ), l = l (Re)

l=64/Re. (5.3)

В этом случае выражение (5.2) принимает вид формулы Пуазейля

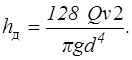
(5.4)

При турбулентном режиме движения (Re > Re_кр) различают три зоны сопротивления.

1. Зона гидравлически гладких труб (Re_кp < Re £ 10 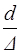; l= l (Re)):

l = 0,3164/Re^0,25 — (5.5)

формула Блазиуса, используемая при Re £ 10⁵ ;

–

формула Конакова, используемая при Re < 3 • 10⁶.

2. Зона шероховатых труб (10d/D < Re £ 500d/D; l=l (Re, D/d):

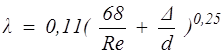–(5.6)

формула Альтшуля.

3. Зона вполне шероховатых труб или квадратичная зона (Re>500d/D; l= l (D/d)):

l=0,11 (D/d)^0,25 – (5.7)

формула Шифринсона.

С незначительной погрешностью формула Альтшуля может исполь­зоваться как универсальная для всей турбулентной области течения. Если живое сечение не имеет формы круга, то формулы (5.2), (5.5), (5.6) и (5.7) могут использоваться при турбулентном движении с заме­ной диаметра трубы d на учетверенный гидравлический радиус R (см. (2.2)) . При ламинарном движении в этом случае используются специаль­ные формулы, приводимые в справочниках.

При решении некоторых типов задач формулу Дарси - Вейсбаха (5.2) удобно представить в виде

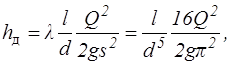(5.8)

где s — площадь живого сечения трубы.

Формула (5.4) является чайным видом выражения (5.8) для лами­нарного течения.

Местными сопротивлениями называются участки трубопрово­да, в которых происходит резкая деформация потока (к ним относятся, в частности, все виды арматуры трубопроводов — вентили, задвижки, тройники, колена и т.д.). Потери напора в местных сопротивлениях h_М определяются по формуле Вейсбаха

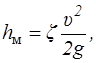(5.9)

где z — коэффициент местного сопротивления, зависящий от его геометрической формы, состояния внутренней поверхности и Re. При развитом турбулентном движении (Re >10⁴), что соответствует квадратичной зоне сопротивления для местных сопротивлений, z_кв = const и определяется по справочникам.

При ламинарном движении значение z можно приближенно вычис­лить по формуле z = z_квj , где j — некоторая функция от Re . Если местных сопротивлений много и расстояние между ними больше длины их взаимного влияния, равного примерно 40d, то потери напора в них суммируются, и расчетная формула (5.9) принимает вид

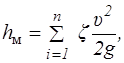(5.10)

где п —число местных сопротивлений; u —средняя скорость потока за местным сопротивлением.

При внезапном расширении потока от сечения площадью s₁ до s₂z_вр можно определить аналитически по формуле z_вр = 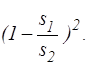Потери напора в местных сопротивлениях можно выразить через экви­валентную длину l_экв , т.е. такую длину трубопровода, для которой h_д=h_м.

L_экв = z d/l. (5.11)

В этом случае выражение (5.11) для h_пот можно представить в виде формулы (5.2) , записав ее следующим образом:

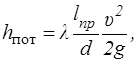(5.12)

где l_пр=l + l_экв называется приведенной длиной.

Если требуется определить не h_пот, а потери давления Δр_пот, то используют формулу

Dp_пот=rgh_пот. (5.13)

Обычно зона деформации потока в районе местного сопротивления мала по сравнению с длиной труб. Поэтому в большинстве задач при­нимается, что потери напора в местном сопротивлении происходят как бы в одном сечении, а не на участке, имеющем некоторую длину.

Вопросы по теме 5.

1 . По каким формулам определяются потери напора в трубах по длине и в местных сопротивлениях?

2. От каких безразмерных величин может зависеть коэффициент гидравлического сопротивления?

3. Каковы границы зон сопротивления при турбулентном течении?

4. Что такое эквивалентная и приведенная длины и когда они упот­ребляются?