Конструктивный расчет

Содержание конструктивного расчета зависит от особенностей выбран­ной конструкции аппарата, т. е. от выбора поверхности теплообмена: трубчатая, пластинчатая, спиральная, ребристая и т. д.

Площадь поверхности теплообмена F,м², определяется из основного уравнения теплопередачи

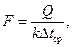(2.36)

где Q – тепловая нагрузка аппарата (определяется из теплового баланса); k – коэффициент теплопередачи; Dt_ср – средняя раз­ность температур.

По поверхности теплообмена подбираются теплообменный аппарат и патрубки.

Для кожухотрубчатых аппаратов, имеющих наибольшее распространение в промышленности, технологических процессах, по поверхности теплообмена F определяются количество труб, их размещение в трубной решетке, диаметр корпуса аппарата, число ходов в трубном и межтрубном пространстве и раз­меры входных и выходных патрубков. Количество труб равно:

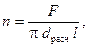(2.37)

где d_расч – расчетный диаметр трубы; при a₁>a₂ d_pacч=d_н,при a₁=a₂ d_pacч= 0,5 (d_н + d_в), при a₁<a₂ d_pacч=d_в; l – длина трубы (выбирается по нормалям).

Трубы в трубных решетках размещаются по вершинам равносторонних треугольников или по сторонам правильных шестиугольников, что одно и то же (ромбическое размещение), и по концентрическим окружностям. Ромби­ческое размещение при большом количестве трубок дает меньшие размеры трубной решетки.

Количество труб в трубных решетках рассчитывается по следующим уравнениям:

(2.38)

где n – общее количество труб; b – количество труб на диагонали наибольшего шестиугольника; а – количество труб на стороне наибольшего шестиугольника.

Шаг труб S (расстояние между осями соседних труб) обычно выбирают равным (1,3–1,5)d_н, но не меньше (d_н+6)мм. Общее количество труб должно быть таким, чтобы а и b были целыми

Внутренний диаметр корпуса аппарата рассчитывают по следующим уравнениям:

для одноходовых аппаратов

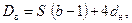(2.39)

или

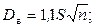(2.40)

для многоходовых аппаратов

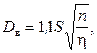(2.41)

где S – шаг труб; п – число труб; η– коэффициент заполнения трубной решетки, η = 0,6÷0,8.

Расчетное значение диаметра корпуса округляется до ближайшего размера, рекомендуемого нормалями.

Диаметры патрубков зависят от скорости и расхода теплоносителей и определяются по формуле

(2.42)

где G – расход (или количество) теплоносителя, кг; r – плотность теплоносителя, кг/м³; ω– скорость теплоносителя в патрубке, м/с.

Скорость теплоносителя в патрубках выбирается по справочнику (чтобы не было кавитационного режима течения). Диаметр патрубка округляется до ближайшего значения, рекомендуемого нормалями.

Внутренний диаметр многоходового теплообменника определяется с учетом размещения перегородок графическим путем или принимается по нормалям.

Расстояние между трубными решетками (активная длина трубок)

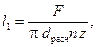(2.43)

где n – число трубок в одном ходе; z – число ходов.

Длина трубок не должна превышать 6 м. В многоходовых аппаратах рекомендуется выбирать четное число ходов. Если при выборе многоходового теплообменника длина труб получается выше допустимой, необходимо изменить диаметр, или скорость движения теплоносителя, или обе эти величины.

Полная высота кожухотрубчатого теплообменника складывается из ак­тивной длины труб и высоты коллекторов

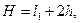(2.44)

где h – высота коллектора. Высоту коллектора выбирают из конструктивных соображений равной 200–400 мм.

Для теплообменника типа «труба в трубе» задаются поверхностью те­плообмена F, количеством секций т, длиной трубы одного элемента l₁.

Определяются:

- длина трубы (при этом задаются количеством параллельно работающих секций m)

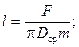(2.45)

- число элементов в каждой секции

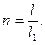(2.46)

Для змеевикового теплообменника исходными данными являются поверх­ность теплообмена F, наружный диаметр трубки d_н, из которой выполнен змеевик, диаметр витка змеевика D_зми расстояние между осями соседних витков S.

Определяются:

- длина трубы, из которой навивается змеевик,

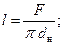(2.47)

- длина одного витка змеевика

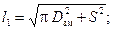(2.48)

- число витков змеевика п=l/l₁.

Для спирального теплообменника исходными данными для конструктив­ного расчета являются поверхность теплообмена F,ширина канала b,тол­щина листов dи высота спиралей h.

Шаг спирали

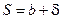, (2.49)

где b = (6÷15) mm; d = (2÷8) мм.

Каждый полувиток спирали строится по радиусам r₁и r₂, которые для первых витков равны:

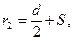(2.50)

где d – диаметр первого витка внутренней спирали (выбирается исходя из конструктивных соображений); r₁ – радиус первого полувитка, r₁ = 140÷150 мм.

Центры, из которых производят построение спиралей, отстоят друг от друга на величину шага витка S.

Длина спирали при числе витков п равна:

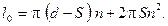(2.51)

Число витков спирали

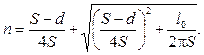(2.52)

Наружныйдиаметр спирального теплообменника

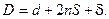(2.53)

Высотаспиралей h принимается по нормалям равной 375¸750 мм.

Диаметры патрубков, м, для входа и выхода теплоносителей определяются по формуле

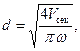(2.54)

где V_сек– секундный расход жидкости, пара или газа, м³/с; ω– скорость жидкости, пара или газа, м/с.

Поверочный расчет

Поверочный расчет производится с целью определения возможности применения имеющихся или стандартных теплообменных аппаратов для необходимых технологических процес­сов. При поверочном расчете заданы размеры аппарата и усло­вия его работы, при этом требуется определить конечные параметры теплоносителей и теплопроизводительность аппарата. Следова­тельно, целью расчета является выбор условий, обеспечиваю­щих оптимальный режим работы аппарата.

В практических условиях наиболее часто требуется определить конечные температуры теплоносителей в готовом или запроектированном теплообменном аппарате при заданных расходах теплоносителей и теплопроизводительности этого аппарата.

Рассмотрим решение данной задачи в условиях теплопередачи без изменения агрегатного состояния теплоносителей, а также при его изменении.

Теплопередача без изменения агрегатного состояния теплоносителей. При решении такой задачи известными величинами являются начальные температуры теплоносителей t₁'и t₂',поверхность нагрева F, значение коэффициента теплопередачи k и значения G₁с₁и G₂с₂. Искомыми величинами являются конечные температуры t₁"и t₂", а также количество переданной теплоты Q. Результат расчета зависит от схемы движения жидкостей.

При прямотоке теплоносителей их конечные температуры t₁" и t₂" могут быть определены по формулам теплопередачи:

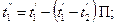(2.55)

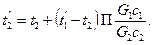(2.56)

Величины П даны в табл. 2.1 в зависимости от отношений G₁с₁/G₂с₂ и kF/G₁с₁. Для противотока конечные температуры теплоносителей оп­ределяются по формулам

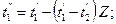(2.57)

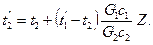(2.58)

Значения Z приведены в табл. 2.2.

Расход теплоты, если известны конечные температуры, определяется в обоих случаях из уравнений теплового баланса (2.5), (2.6).

Таблица 2.1

Значения функции П в уравнениях (2.55) и (2.56)

G1с1/G2с2	kF/G1с1
0,033	0,10	0,33	0,50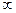
	0,033	0,10	0,28	0,39	0,63	0,86	0,96	1,00
0,01	0,033	0,10	0,28	0,39	0,63	0,86	0,95	0,99
0,05	0,033	0,10	0,28	0,39	0,62	0,84	0,91	0,95
0,10	0,033	0,10	0,28	0,38	0,61	0,81	0,89	0,91
0,20	0,033	0,10	0,27	0,38	0,58	0,76	0,81	0,83
0,50	0,033	0,10	0,26	0,35	0,52	0,63	0,66	0,67
1,0	0,033	0,09	0,25	0,32	0,43	0,49	0,50	0,50
Продолжение табл. 2.1
2,0	0,033	0,09	0,21	0,26	0,32	0,33	0,33	0,33
5,0	0,032	0,08	0,14	0,16	0,17	0,17	0,17	0,17
10,0	0,028	0,06	0,09	0,09	0,09	0,09	0,09	0,09
20,0	0,024	0,04	0,05	0,05	0,05	0,05	0,05	0,05
50,0	0,016	0,02	0,02	0,02	0,02	0,02	0,02	0,02
100,0	0,009	0,01	0,01	0,01	0,01	0,01	0,01	0,01

Таблица 2.2

Значения функции Z в уравнениях (2.57) и (2.58)

G1с1/G2с2	kF/G1с1
0,033	0,10	0,33	0,50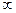
	0,033	0,10	0,28	0,39	0,63	0,86	0,95	1,00
0,01	0,033	0,10	0,28	0,39	0,63	0,86	0,95	1,00
0,05	0,033	0,10	0,28	0,39	0,62	0,86	0,94	1,00
0,10	0,033	0,10	0,28	0,38	0,61	0,85	0,94	1,00
0,20	0,033	0,10	0,28	0,38	0,60	0,83	0,93	1,00
0,50	0,033	0,10	0,26	0,36	0,57	0,78	0,89	1,00
1,00	0,033	0,10	0,25	0,34	0,51	0,68	0,77	1,00
2,0	0,033	0,09	0,23	0,29	0,39	0,46	0,49	0,50
5,0	0,032	0,08	0,16	0,18	0,20	0,20	0,20	0,20
10,0	0,028	0,06	0,10	0,10	0,10	0,10	0,10	0,10
20,0	0,024	0,04	0,05	0,05	0,05	0,05	0,05	0,05
	0,016	0,02	0,02	0,02	0,02	0,02	0,02	0,02
100,0	0,010	0,01	0,01	0,01	0,01	0,01	0,01	0,01

Формулы (2.55) и (2.57) обладают тем недостатком, что они применимы лишь к двум наиболее простым схемам движения теплоносителей. Кроме того, при выводе формул предполагается независимость теплоемкостей массового расхода теплоносителей от температуры, хотя это далеко не всегда соответствует реальным условиям. Кроме того, точно определить значение коэффициента теплопередачи, не зная конечных температур теплоносителей, нельзя. Поэтому весьма часто не удается использовать приведенные выше формулы для поверочного расчета. В таких случаях расчет приходится вести методом последовательных приближений. При этом задаются конечными температурами и производится расчет в порядке приведенного выше конструктивного расчета. Если полученная в результате этого расчета поверхность нагрева совпадает с действительной, то расчет на этом заканчивается, так как данное совпадение свиде­тельствует о том, что конечные температуры выбраны правильно. В противном случае расчет приходится производить снова, задавшись иными значениями конечных температур.

Теплопередача при изменении агрегатного состояния теплоносителей. Если проходящая через аппарат жидкость нагрева­ется за счет теплоты конденсации пара, то характер изменения температуры жидкости по длине поверхности нагрева соответ­ствует графику, приведенному на рис. 2.12.

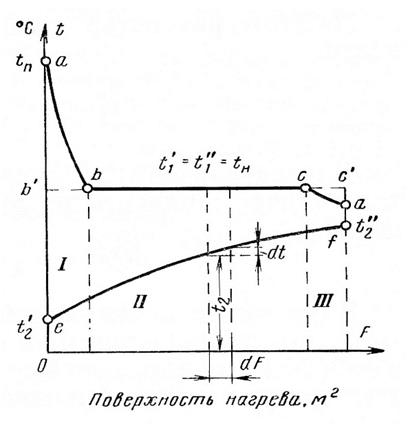
Рис. 2.12. Изменение температур греющего параи подогреваемой воды по поверхноститеплообменника:

I –область перегретого пара; II – область насыщенного пара; III – область переохлажденного конденсата; abcd – кривая изменения температуры греющего теплоносителя; ef – кривая изменения температуры жидкости

Уравнение для этого графика в координатах t и F можносоставить, исходя из следующих соображений. При пере­мещении G, кг/с, жидкости вдоль элементарной поверхности нагрева dF температура ее изменяется на величину dt.Коли­чество теплоты, передаваемое от конденсирующегося пара к жидкости через эту элементарную поверхность, может быть выражено уравнением

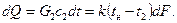(2.59)

Разделив переменные и проинтегрировав обе части уравнения в соответствующих пределах, получим:

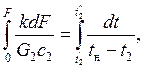
или

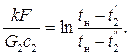
Из этого равенства определяется конечная температура жид­кости:

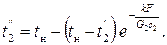(2.60)

Для случая кипения жидкости за счет теплоты горячего газа или горячей жидкости по аналогии с предыдущим имеем урав­нение

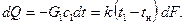(2.61)

Знак минус перед членами, содержащими dt, поставлен по­тому, что приращения dt и dF имеют разные знаки. Из уравне­ния (2.61) аналогично предыдущему определяется конечная температура греющей жидкости или газа:

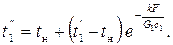(2.62)

Промежуточные значения температур определяются путем подстановки в выражения для конечных температур соответ­ствующих значений F. Наименьшее давление пара, при конден­сации которого возможен нагрев жидкости или газа до желае­мой температуры t₂",определяется исходя из того, что темпера­тура насыщения t_н, соответствующая этому давлению, должна быть больше, чем t₂",на некоторую величину dt.