РАСЧЕТЫ РЕКУПЕРАТИВНЫХ ТЕПЛООБМЕННЫХ

АППАРАТОВ

Тепловой расчет

Тепловой расчет начинается с определения тепловой на­грузки аппарата и расхода одного из теплоносителей. Тепловой нагрузкой называется количество теплоты, переданное от горя­чего теплоносителя к холодному. Тепловая нагрузка опреде­ляется из уравнения теплового баланса и в идеальном случае определяется по формуле:

. (2.4)

Общий вид уравнения теплового баланса:

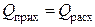. (2.5)

В зависимости от заданного процесса уравнения тепловых балансов имеют различный вид.

Для подогревателей.Если нагрев одного из теплоносителей происходит за счет охлаждения другого теплоносителя, т.е. ап­парат работает без изменения агрегатного (фазового) состояния теплоносителей, то уравнения теплового баланса имеют вид:

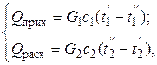(2.6)

где G₁и G₂ – массовые расходы теплоносителей (воздуха, га­зов и т.п.), не изменяющих агрегатного состояния; с₁и с₂– теплоемкости теплоносителей; t₁', t₂', t₁" и t₂" – начальные и ко­нечные температуры теплоносителей.

Уравнение теплового баланса с учетом потерь:

(2.7)

где Q_пот – потери теплоты от стенок аппарата в окружающую среду.

Из практики известно, что тепловые потери составляют обычно 2–3 % количества подведенного тепла.

Их можно учесть коэффициентом η = 0,97÷0,98:

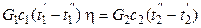. (2.8)

В этом случае расход греющего теплоносителя выразится как

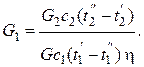(2.9)

Для компактных конструкций величина тепловых потерь зна­чительно меньше и не достигает даже 1 %. Тепловые потери изо­лированных теплообменников пропорциональны их наружной поверхности и ограничены ее предельно допустимой температу­рой.

Если нагрев одного из теплоносителей происходит за счет конденсации греющего водяного насыщенного пара, то

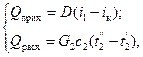(2.6а)

где D – количество греющего пара; i₁– энтальпия греющего пара (определяется из таблиц насыщенного водяного пара); i_K– энтальпия конденсата, i_K= c_вt_к; G₂ – масса (или массовый рас­ход) нагреваемого вещества; с₂– теплоемкость нагреваемого вещества; t₂' – начальная температура нагреваемого вещества; t₂" – конечная температура нагреваемого вещества.

Уравнение теплового баланса с учетом потерь:

, (2.7а)

где Q_пот – потери теплоты от стенок аппарата в окружающую среду.

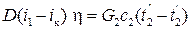. (2.8а)

В этом случае расход греющего пара выразится как

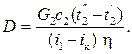(2.9а)

Для испарителей.Нагрев и охлаждение теплоносителей со­провождаются изменением их агрегатного состояния, например, насыщенный пар, нагревая воду до состояния кипения и после­дующего интенсивного испарения, сам конденсируется:

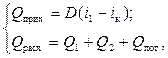(2.10)

где Q₁ – теплота, израсходованная на нагрев холодного тепло­носителя до температуры кипения; Q₂ – теплота, затраченная на испарение кипящей жидкости:

(2.11)

где G₂ – количество (или расход) холодного теплоносителя; с₂ – средняя теплоемкость теплоносителя; t_s – температура кипения холодного теплоносителя; t₂' – начальная температура холод­ного теплоносителя; r – скрытая теплота испарения теплоно­сителя.

Уравнение теплового баланса:

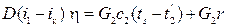(2.12)

Расход греющего пара

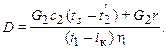(2.13)

При наличии продувки испарителя следует учесть потерю тепла с продувкой.

Для конденсаторов. В аппаратах этого типа более нагретый теплоноситель охлаждается с изменением агрегатного состояния. Например, пары аммиака, охлаждаясь, конденсируются, и жидкий аммиак выходит с заданной температурой. Теплота от горячего теплоносителя чаще всего отводится холодной водой:

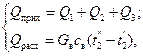(2.14)

где Q₁ – теплота, выделяющаяся при охлаждении перегретых паров до насыщенного состояния; Q₂– теплота, выделяющаяся при конденсации насыщенного пара; Q₃ – теплота, выделяю­щаяся при охлаждении горячей жидкости до заданной темпе­ратуры; G_B– расход охлаждающей воды:

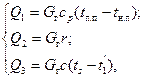(2.15)

где G_г– количество горячего теплоносителя; с_р – теплоемкость при постоянном давлении для перегретого пара; t_п.п – темпера­тура перегретого пара; t_н.п – температура насыщенного пара; r – скрытая теплота конденсации горячего теплоносителя; с – теплоемкость жидкого горячего теплоносителя; t_s – температура кипения горячего теплоносителя; t₂' – конечная температура го­рячего теплоносителя.

Уравнение теплового баланса:

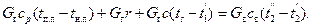(2.16)

Если охлаждающая вода подается в межтрубное простран­ство и внешние стенки аппарата имеют температуру, мало от­личающуюся от температуры окружающей среды, то тепловыми потерями вследствие их малости пренебрегают.

Расход охлаждающей воды определяется из уравнения теп­лового баланса:

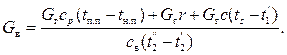(2.17)

Для холодильников

(2.18)

где G_гор – количество горячего теплоносителя; с – средняя теп­лоемкость горячего теплоносителя; t₁' – начальная температура горячего теплоносителя; t₁" – конечная температура горячего теплоносителя; G_хол – расход (или количество) охлаждающей воды; с_в – средняя теплоемкость охлаждающей воды; t₂" – тем­пература охлаждающей воды на выходе из аппарата; t₂' – тем­пературы охлаждающей воды на входе в аппарат.

Уравнение теплового баланса:

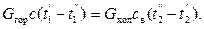(2.19)

Из уравнения теплового баланса определяется расход ох­лаждающей воды:

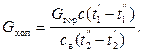(2.20)

Если в процессе теплообмена происходит дополнительный подвод или отвод теплоты, например, за счет химической реак­ции или фазовых и других превращений вещества, то их также необходимо учесть в тепловом балансе.

Следующим этапом теплового расчета является расчет температурного режима работы теплообменного аппа­рата, который состоит из определения средних температур теплоносите­лей и средней разности температур Dt_ср, а также стенок аппа­рата.

Приступая к расчету температурного режима теплообмен­ника, необходимо сначала установить характер изменения тем­пературы теплоносителей, а также выбрать схему их движения так, чтобы получить максимальную среднюю разность температур. Это создает наилучшие условия для теплопередачи.

Направления движения теплоносителей 1 и 2 могут быть прямоточными, противоточными, перекрестными и смешанного тока (со сложным направлением движения теплоносителей) (рис. 2.9).

Рис. 2.9. Схемы движения теплоносителей в теплообменниках:

а – прямоток; б – противоток; в – перекрестный ток; г – прямоток и противоток одновременно; д – многократно перекрестный ток

Характер изменения температур теплоносителей вдоль поверхности теплообмена определяется схемой движения и соотношением теплоемкостей массовых расходов теплоносите­лей. На рис. 2.10 представлены графики изменения температур для трех возможных соотношений теплоемкостей и массовых расходов теплоносителей.

Если температура обоих теплоносителей изменяется вдоль поверхности теплообмена, то при противотоке и прямотоке

(2.21)

где Dt_б и Dt_м – большая и меньшая разности температур между первичными и вторичными теплоносителями на концах тепло­обменника.

Полученная разность температур (2.21) называется средне-логарифмическим температурным напором. Формула (2.21) справедлива для простейших схем аппаратов при условии по­стоянства массового расхода теплоносителей и коэффициента теплопередачи вдоль всей поверхности теплообмена.

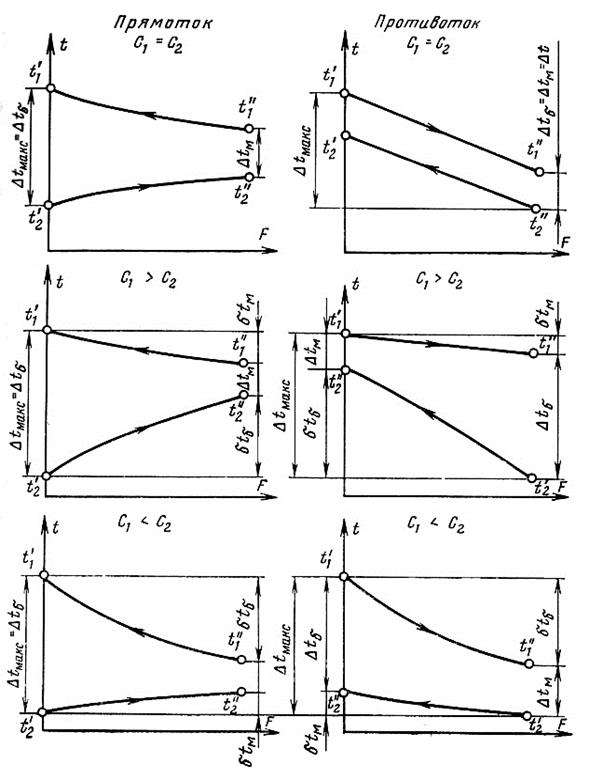
Рис. 2.10. График изменения температур теплоносителей по поверхности ап­парата при их прямотоке и противотоке

Расчет средней разности температур для сложных схем дви­жения теплоносителей производят следующим образом: вначале опре­деляют температурный напор по формуле (2.21), а затем находят вспомогательные величины

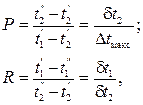(2.22)

где dt₁ и dt₂– приращение темпера­туры горячего и холодного теплоно­сителя.

Величина Р представляет собой отношение степени нагрева холод­ной среды к максимально возмож­ному перепаду температур, вели­чина R – отношение степени охлаждения горячей среды к сте­пени нагрева холодной среды.

В зависимости от величин Р и R из графика, представленного на рис. 2.11, определяют поправку e_Dt = f (Р, R). Температурный напор на­ходится как

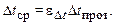(2.23)

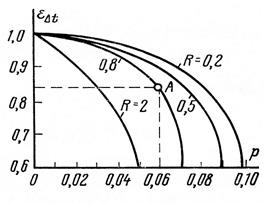
Рис. 2.11. Графики для опреде­ления поправочного коэффи­циента

В тех случаях, когда температура теплоносителей вдоль по­верхности теплообмена изменяется незначительно, средняя раз­ность температур вычисляется по упрощенной формуле как средняя арифметическая крайних напоров:

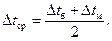(2.24)

Так как значения среднеарифметического температурного напора всегда больше, чем среднелогарифмического, то расчет по формуле (2.24) справедлив при Dt_б/Dt_м <2. При периодиче­ском процессе охлаждения средняя разность температур подсчитывается по формуле

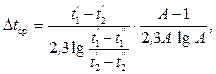(2.25)

где t₁^' – начальная температура охлаждаемой жидкости; t₁" – конечная температура охлаждаемой жидкости; t₂' – начальная температура охлаждающей жидкости; t₂'' – конечная температура охлаждающей жидкости.

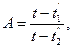(2.26)

где t – температура охлаждающей жидкости в любой момент времени.

Средняя разность температур при периодическом процессе нагревания подсчитывается по формуле

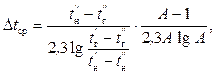(2.27)

где t_н' – начальная температура нагреваемой жидкости; t_н" – конечная температура нагреваемой жидкости; t_г' – начальная температура греющей жидкости; t_г" – конечная температура греющей жидкости;

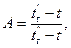(2.28)

где t – температура нагреваемой жидкости в любой момент времени, °С.

Если аппарат имеет несколько зон (например, конденсатор паровой турбины), то среднюю разность температур подсчитывают для каждой зоны отдельно. Важное значение имеет средняя температура теплоносителей, поскольку именно при этой температуре вычисляется коэффициент теплопередачи.

Температура стенки зависит от средних температур рабочих сред и условий теплообмена. Для расчета используется уравнение

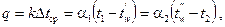(2.29)

где q – удельный тепловой поток или тепловая нагрузка; k – коэффициент теплопередачи; Dt_ср – средняя разность температур или температурный напор; a₁ – коэффициент теплоотдачи от горячей воды к стенке; a₂ – коэффициент теплоотдачи от стенки к холодной среде; t₁– средняя температура горячей среды; t_w' – температура стенки со стороны горячей среды; t_w" – температура стенки со стороны холодной среды; t₂– средняя температура холодной среды.

Тогда

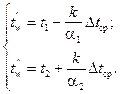(2.30)

Отношением k/a предварительно задаются, а затем прове­ряют соответствие его расчетному значению. Пересчет позво­ляет получить соответствие принятого значения расчетному.

Коэффициент теплопередачи k представляет собой количест­венную расчетную величину, характеризующую сложный тепло­обмен. Он зависит от коэффициентов теплоотдачи, термического сопротивления стенки и загрязнений. Для плоской стенки

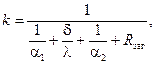(2.31)

где a₁ – коэффициент теплоотдачи от горячего теплоносителя; d – толщина стенки аппарата; l – коэффициент теплопроводно­сти материала стенки; a₂– коэффициент теплоотдачи от стенки к холодному теплоносителю; R_заг– термическое сопротивление, учитывающее загрязнение с обеих сторон стенки (накипь, сажа и пр.), м²∙К/Вт.

Для стенки, имеющей другие геометрические формы (ци­линдрической, шаровой, многослойной плоской, многослойной цилиндрической, многослойной шаровой, ребристой и т. д.), рас­четные формулы для определения коэффициента теплопередачи можно, найти в справочной литературе. Если стенка трубы тон­кая, то с достаточной степенью точности можно проводить расчет по формуле для плос­кой стенки. Так, при d_вн/d_нар<2 погрешность не превышает 4 %.

Если теплопроводность слоя загрязнения неизвестна, то рассчи­тывается коэффициент теплопередачи k для чистой стенки и вво­дится поправка на ее загрязнение при помощи коэффициента ис­пользования поверхности теплообмена φ:

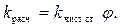(2.32)

Для большинства аппаратов числовое значение коэффи­циента φ лежит в пределах φ = 0,65÷0,85. В случае большого выпадения осадков из теплоносителей на поверхности теплооб­мена коэффициент φ = 0,4÷0,5.

Коэффициенты теплоотдачи a определяются в большинстве случаев с помощью критерия Нуссельта:

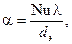(2.33)

где Nu – безразмерный критерий подобия – критерий Нусcельта; l– коэффициент теплопроводности того теплоносителя, длякоторого определяется коэффициент теплоотдачи; d_э– эквивалентный диаметр, определяемый по формуле:

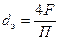(2.34)

где F – площадь поперечного сечения; П – смоченный пери­метр.

Критерий Nu вычисляется в зависимости от характера дви­жения и агрегатного состояния теплоносителей по критериальнымуравнениям различного вида.

Для расчета среднего коэффициента теплоотдачи при турбулентном течении различных жидкостей (кроме жидких металлов) для диапазона чисел Рейнольдса Re = 10⁴÷5∙10⁶ используется следующее критериальное уравнение:

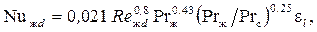(2.35)

где Re_жd – критерий Рейнольдса, определенный при темпера­туре жидкости и определяющем размере трубы; Рг_ж – критерий Прандтля, определенный при температуре жидкости; Рг_с – кри­терий Прандтля, определенный при температуре стенки; e_l – коэффициент, учитывающий изменение среднего коэффициента теплоотдачи по длине трубы: при l/d≥50 e_l = l, при l/d<50 не­обходимо учитывать влияние начального термического участка. Значения e_l в зависимости от числа Re и отношения l/d приведены в справочной литературе.

В уравнении (2.35) за определяющую температуру принята средняя температура жидкости, а за определяющий размер – внутренний диаметр трубы. Диапазон значений критерия Прандтля, удовлетворяющий этому уравнению, довольно широк и составляет Рr = 0,6÷2500.