Расчет контура регулирования напряжения

Структурная схема первого внутреннего контура представлена на рис. 5.6. Здесь 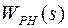- передаточная функция РН, 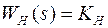- ПФ делителя напряжения.

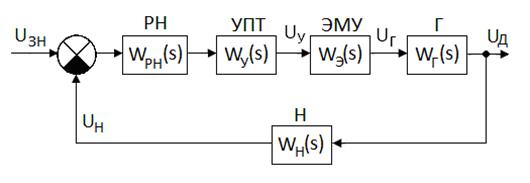
Рис. 5.6. Структурная схема контура регулирования напряжения

В соответствии с методикой подчиненного регулирования координат внутренние контуры настраиваются по быстродействию на так называемый модульный оптимум, которому соответствует желаемая ПФ разомкнутой системы следующего вида

,

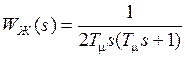где 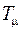– нескомпенсированная постоянная времени.

В качестве 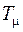берется наименьшая постоянная времени синтезируемого контура, поэтому она часто называется малой постоянной времени. По существу 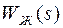– ПФ реального интегратора. При этом желаемая ПФ замкнутой системы определяется соотношением

,

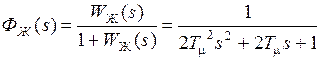т.е. представляет собой колебательное звено с незначительным коэффициентом демпфирования .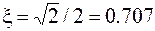

Такой настройке соответствуют высокие динамические показатели качества - перерегулирование 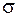и длительность переходного процесса 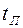достаточно малы 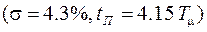, а точность приемлема, так как контур обладает астатизмом первого порядка.

Возьмем в качестве нескомпенсированной постоянной времени 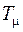постоянную времени обмотки уравнения ЭМУ, т.е. положим 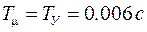. Тогда желаемая ПФ разомкнутого контура будет иметь следующий вид:

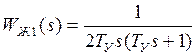
Зададимся значением коэффициента передачи датчика напряжения 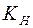, исходя из следующих соображений. Максимальное напряжение цепи обратной связи 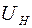, подаваемого на РН, ограничим значением 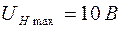при максимальном значении напряжения генератора 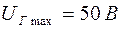, которое равно максимальному напряжению, подаваемому на электродвигатель. Отсюда будем иметь

.

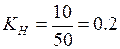Теперь можно определить ПФ разомкнутого контура :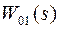

.

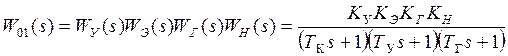После этого рассчитаем ПФ регулятора напряжения 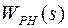по соотношению

.

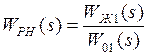В результате получим

,

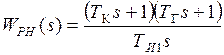где 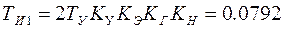с – постоянная времени интегрирования РН.

Поделив числитель ПФ 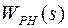на ее знаменатель, определим параллельную структуру РН:

,

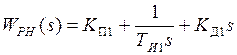где 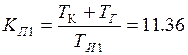– коэффициент передачи пропорционального звена;

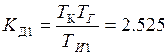с – коэффициент передачи дифференциатора.

Анализ показывает, что РН реализует пропорционально - интегрально - дифференциальный (ПИД) закон управления.