Построение дискретных моделей непрерывных систем

Для преобразования непрерывных моделей в дискретные в состав Control System Toolbox включена функция c2d, основная форма обращения к которой имеет следующий вид:

sysd=c2d(sysc, T_s),

где sysc, sysd – соответственно идентификаторы исходного непрерывного и создаваемого дискретного объектов. В этой форме по умолчанию используется схема выборки с фиксатором нулевого порядка, который реализует основной способ экстраполяции квантованного сигнала в дискретно-непрерывных системах управления.

Пример 1.12. Построение эквивалентной дискретной zpk-модели w12d для непрерывного объекта с ПФ

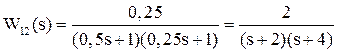
при T_s=0.15c и использовании экстраполятора нулевого порядка.

>> w12=zpk([], [-2 -4], 2); % создание zpk-модели

>> w12d=c2d(w12, 0.15) ; % переход к дискретной zpk-модели

Zero/pole/gain:

0.016794 (z+0.7408)

(z-0.7408) (z-0.5488)

Sampling time: 0.15

Задание 1.12. Сформируйте дискретную zpk-модель h12d для непрерывного объекта с ПФ

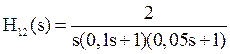
при наличии на его входе ключа с фиксатором нулевого порядка и T_s=0,1c.

В задачах переоборудования непрерывных регуляторов в дискретные часто используется аппроксимация Тастина, которая связана с подстановкой в непрерывную передаточную функцию W(s) выражения 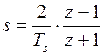. Соответствующая этому способу функция c2d имеет следующую форму:

sysd=c2d(sysc, T_s, 'tustin'),

где 'tustin' – идентификатор метода.

Пример 1.13.Построение эквивалентной дискретной zpk-модели с использованием аппроксимации Тастина для непрерывного объекта с ПФ W₁₂(s) и T_s=0,15c.

>> w13=c2d(w12, 0.15, 'tustin')

Zero/pole/gain:

0.0075251 (z+1)^2

(z-0.7391) (z-0.5385)

Sampling time: 0.15

Задание 1.13. Сформируйте дискретную zpk-модель h13 для объекта с ПФ H₁₂(s) с использованием аппроксимации Тастина и T_s=0,1c.

Если требуется согласовать характеристики непрерывной и дискретной моделей на некоторой частоте ω_c, то применяют билинейную аппроксимацию Тастина с коррекцией

,

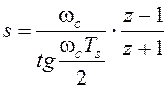которая реализована в следующей форме функции c2d:

sysd=c2d(sysc, T_s,'prewarp', ω_c),

где 'prewarp' – идентификатор метода аппроксимации Тастина с коррекцией на частоте ω_c.

Пример 1.14.Построение дискретной zpk-модели на основе ПФ W₁₂(s) с применением аппроксимации Тастина c коррекцией на частоте ω_c=3с^-1 при T_s=0,15c:

>> w14=c2d(w12, 0.15, 'prewarp', 3)

Zero/pole/gain:

0.0077383 (z+1)^2

(z-0.7352) (z-0.5324)

Sampling time: 0.15

Задание 1.14. Сформируйте дискретную tf-модель h14 на основе H₁₂(s) с использованием аппроксимации Тастина с коррекцией на частоте ω_c=5с^-1 при T_s=0,1c.

Функция c2d позволяет строить дискретные модели для непрерывных систем с запаздыванием при условии использования в качестве экстраполятора фиксатора нулевого и первого порядков.

Пример 1.15. Созданный ранее объект w11 (с запаздыванием τ = 0,25 с) можно преобразовать в дискретную tf-модель с T_s=0,15c следующей командой:

>> w15=c2d(w11, 0.15)

Transfer function:

0.02419 z^2 + 0.2853 z + 0.07928

z^(-1) *

z^3 - 1.741 z^2 + 0.7408 z

Sampling time: 0.15

Задание 1.15. Постройте эквивалентную дискретную модель h15 на основе ранее сформированной непрерывной модели с запаздыванием h11 при T_s = 0,1с.