Формирование дискретных lti-объектов

Для создания дискретной модели с заданным периодом квантования к входным аргументам функций tf,zpk иss добавляется период дискретности T_s, измеряемый в секундах:

sys=tf(num,den,T_s),

sys=zpk(z,p,k, T_s),

sys=ss(a,b,c,d, T_s).

Пример 1.7. Формирование дискретной модели w7 по передаточной функции

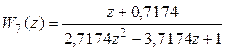при T_s=0,1.

>> w7=tf([1 0.7174], [2.7174 -3.7174 1], 0.1)

Transfer function:

z + 0.7174

2.717 z^2 - 3.717 z + 1

Sampling time: 0.1

Задание 1.7. Создайте дискретную модель h7 подкласса tf по передаточной функции Н₇(z) при T_s=0.2 с:

.

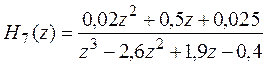Оператор sys=ss(a,b,c,d, T_s) формирует модель дискретной системы в пространстве состояний следующего вида:

x[(n+1) T_s]=Ax[n T_s]+Bu[n T_s];

y[nT_s]=Cx[nT_s]+Du[n T_s],

где n=0,1,2, ... – целочисленный аргумент (дискретное время), T_s - период квантования, который для упрощения записи уравнений состояния часто опускают.

Пример 1.8. Создание дискретной ss-модели с периодом квантования T_s =0,1 с, заданной четверкой матриц A, B, C, D:

; ;

;

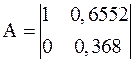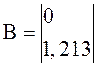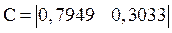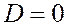
>> sys8=ss([1 0.6552; 0 0.368],[0; 1.213], [0.7949 0.3033], 0, 0.1)

a = x1 x2

x1 1 0.6552

x2 0 0.368

b = u1

x1 0

x2 1.213

c = x1 x2

y1 0.7949 0.3033

d = u1

y1 0

Sampling time: 0.1

Discrete-time model.

Задание 1.8. Сформировать дискретную модель h8 в пространстве состояний, заданную матрицами A, B, C, D и периодом дискретности T_s=0,2 с:

; ;

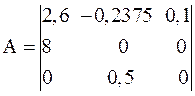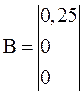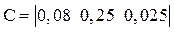; D=0.

В Control System Toolbox принято, что период дискретности T_s=0 соответствует непрерывной системе, а значение T_s= -1 - случаю, когда период квантования для дискретной системы не специфицирован.

Пример 1.9.Формирование дискретной zpk-модели без приписки значения периоду дискретности для объекта с дискретной ПФ:

.

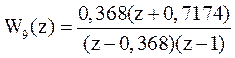>> w9=zpk(-0.7174, [0.368 1], 0.368, -1)

Zero/pole/gain: 0.368 (z+0.7174)

(z-0.368) (z-1)

Sampling time: unspecified

Задание 1.9. Сформируйте дискретную модель h9 в zpk-форме по передаточной функции Н₉(z) для неспецифицированного периода дискретности T_s:

.

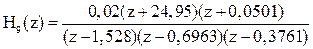В ряде задач дискретные передаточные функции принято записывать как рациональные выражения от аргумента z^-1 (dsp–форма), например:

.

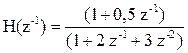Для формирования дискретной ПФ в dsp-форме используется функция filt, которая по существу создает объекты подкласса tf. Возможны два способа обращения к функции filt:

h= filt(num, den);

h= filt(num, den, T_s).

Первый способ используется для формирования дискретной ПФ, которой не приписывается период квантования; второй – при заданном периоде квантования T_s.

Пример 1.10. Создание модели w10 подкласса tf с неспецифицированным периодом дискретности для объекта с передаточной функцией

.

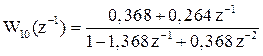>> w10=filt([0.368 0.264], [1 -1.368 0.368])

Transfer function: 0.368 + 0.264 z^-1

1 - 1.368 z^-1 + 0.368 z^-2

Sampling time: unspecified

!! Задание 1.10. Сформируйте дискретную модель h10 в dsp-форме для объекта с передаточной функцией:

H₁₀(z^-1)= 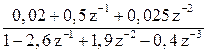, при T_s=0,5с.