Формирование tf-объектов

ТЕОРИЯ АВТОМАТИЧЕСКОГО

УПРАВЛЕНИЯ В СРЕДЕ MATLAB

Учебное пособие

Самара

Самарский государственный технический университет

Печатается по решению редакционно-издательского совета СамГТУ

УДК 681.51

Будин В. И.

Теория автоматического управления в среде MATLAB: учеб. пособие / В. И. Будин, Ф. В. Дремов. – Самара: Самар. гос. техн. ун-т, 2014. – 127 с.: ил. 36, табл. 7. Библиогр.: 9 назв.

Излагаются функциональные возможности системы MATLAB с ее основными приложениями Control System Toolbox и Simulink, которые ориентированы на решение задач теории автоматического управления. Материал сопровождается значительным количеством примеров. Приводятся контрольные вопросы и упражнения для самостоятельного решения.

Для студентов технических вузов всех форм обучения, изучающих дисциплину «Теория автоматического управления» по программам направлений бакалавриата «Автоматизация технологических процессов и производств» и «Электроэнергетика и электротехника (профиль - Электропривод и автоматика промышленных установок)». Может быть также полезно при выполнении выпускных квалификационных работ по данным направлениям.

УДК 681.51

Рецензенты: зам. начальника кафедры АРЭО ВУНЦ ВВС "ВВА"

к.т.н. Алексеев Э.О.;

доцент кафедры «Электромеханика и промышленная

автоматика» Сф СамГТУ к.т.н. Горшков Р.Г.

Ó В. И. Будин, Ф. В. Дремов, 2014

Ó Самарский государственный

технический университет, 2014

ПРЕДИСЛОВИЕ

Предлагаемое учебное пособие написано в соответствии с требованиями Федерального государственного образовательного стандарта для высшего профессионального образования к уровню подготовки бакалавров направлений «Автоматизация технологических процессов и производств» и «Электроэнергетика и электротехника» по дисциплине «Теория автоматического управления» с целью самостоятельного изучения пакета научно-инженерских расчетов MATLAB и его практического применения для решения задач анализа и синтеза автоматических систем, в том числе, освоение способов построения моделей динамических объектов и систем непрерывного и дискретного управления в среде MATLAB, формирование устойчивых навыков использования функций и команд приложений пакета MATLAB для исследования и проектирования систем автоматического управления во временной и частотной областях, освоение методов машинного моделирования нелинейных систем и их параметрическая оптимизация с использованием Simulink.

Данное пособие является дополнением к учебникам по теории автоматического управления и имеет практическую направленность. Особенно оно полезно студентам при выполнении дипломного проекта и курсовых работ, связанных с проектированием автоматических систем.

В пособии основной упор делается на получение и закрепление устойчивых навыков применения MATLAB: в каждом разделе приводится большое количество примеров, иллюстрирующих использование функций и команд MATLAB; в практической части каждой темы предлагается самостоятельное выполнение значительного количества заданий; каждая глава заканчивается объемным дополнительным упражнением и контрольными вопросами.

Начинать изучение материала пособия целесообразно с первой главы, т.к. он выстроен в соответствии с принципами последовательного перехода от известной информации к новой, от простого материала к более сложному, что позволяет наиболее быстро получить практические навыки даже начинающему пользователю MATLAB, не имеющего опыта работы в этой среде. При этом рекомендуется использовать все версии MATLAB выше 7.1, т.к. интерфейс среды более ранних версий пакета несколько отличается, что может вызвать некоторые затруднения при выполнении заданий и упражнений.

ВВЕДЕНИЕ

Развитие теории автоматического управления (ТАУ) в последнее десятилетие показывает, что наиболее эффективные методы анализа и синтеза автоматических систем ориентированы на использование ЭВМ. В инженерной практике среди математических компьютерных систем наибольшее распространение получил пакет MATLAB, который имеет значительное количество специальных приложений (Toolbox) для решения задач исследования и проектирования систем автоматического управления (САУ). Среди них можно особо выделить Control System Toolbox и Simulink. Эти приложения являются основным инструментом специалистов в области машинного анализа и синтеза автоматических систем. В большинстве зарубежных изданий по ТАУ среда MATLAB используется как средство решения сложных с вычислительной точки зрения задач, встречающихся при проектировании САУ, в том числе создание математических моделей объектов и систем в целом, их преобразование, расчет динамических процессов и определение точности в установившихся режимах работы систем регулирования.

Следует отметить, что современная теория автоматического управления, в основе которой лежат математические модели управления в виде матричных дифференциальных уравнений практически не применимы без использования системы MATLAB из-за сложности вычислительных процедур.

MATLAB по существу создавался как система научно-инженерных расчетов, ядром которой являются операции над матрицами. Это предопределило аббревиатуру пакета MATrix LABoratory (матричная лаборатория). Поэтому современное направление ТАУ в виде метода пространства состояний в значительной мере опирается на вычислительно-алгоритмическое обеспечение системы MATLAB и указывает в свою очередь пути совершенствования и разработки ее новых приложений.

В области автоматизированного проектирования систем автоматического управления в настоящее время наибольшее внимание уделяется созданию в вычислительных средах динамических моделей. Поэтому в предлагаемом пособии в первую очередь рассматривается тема формирования в среде MATLAB типовых математических моделей объектов и систем с помощью приложения Control System Toolbox. Он позволяет создавать модели трех классов: два типа на основе передаточных функций (ПФ) и один на основе стандартной формы уравнений состояния. Все эти объекты однозначно взаимосвязаны, имеют определенные приоритеты и могут использоваться для преобразования структурных схем САУ и анализа динамических и статических свойств разрабатываемых систем управления. В этом разделе рассматриваются также вопросы дискретизации непрерывных моделей, создания моделей с запаздыванием и дискретных систем с амплитудно-импульсной модуляцией.

Второй раздел посвящен изучению и приобретению навыков исследования САУ в среде MATLAB. В основном это решение задач по оценке динамических параметров систем регулирования, расчету переходных и весовых характеристик, получению частотных характеристик разомкнутых и замкнутых САУ, в том числе в логарифмическом масштабе. Ранее это считалось сложной трудоемкой рутинной работой. Использование среды MATLAB исключает эту проблему. Приводимые функции и команды приложения Control System Toolbox позволяют значительно упростить решение задач анализа линейных САУ.

В третьем разделе рассматриваются вопросы использования Simulink для исследования нелинейных САУ. Это самое объемное приложение MATLAB, которое, по существу, с добавлением ядра MATLAB приобретает свойства самостоятельного пакета, предназначенного для моделирования динамических систем. В его основе лежат принципы визуального программирования, благодаря чему модель САУ набирается в виде схемы, состоящей из отдельных типовых блоков. Такая структура позволяет исследовать динамические свойства автоматических систем сразу по нескольким «физическим» координатам с учетом их ограничений и влияния нелинейностей статистических характеристик отдельных звеньев. В основе вычислительных процессов моделирования в Simulink лежат численные методы интегрирования дифференциальных уравнений в виде разностных схем Рунге-Кутты. В качестве метода интегрирования для неопытного пользователя рекомендуется использовать схему, предлагаемую по умолчанию.

При проектировании САУ полученный регулятор, как правило, требует параметрической настройки по заданному критерию качества. Для решения этой задачи в пакет MATLAB встроено приложение Simulink Response Optimization, которому посвящен четвертый раздел пособия. Этот программный продукт интегрирован с Simulink и по существу построен на использовании его модельной схемы. Настройка осуществляется путем одновременной минимизации перерегулирования и длительности переходного процесса по вычисляемым при поиске оптимума переходным характеристикам путем их вписывания в специальную зону, формируемую по заданным показателям качества. Поиск оптимальных настроек регулятора может осуществляться сразу по нескольким параметрам одновременно. При этом учитывается нестабильность параметров объекта управления и системы в целом.

В последнем (пятом) разделе предлагается пример проектирования следящей системы с применением рассмотренных функциональных возможностей приложений пакета MATLAB. При этом синтез управляющего устройства осуществляется с применением методики построения многоконтурных систем с подчиненным регулированием координат. На всех этапах проектирования этой САУ используется среда MATLAB.

1. ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ С ПОМОЩЬЮ ПАКЕТА CONTROL SYSTEM TOOLBOX

Пакет Control System Toolbox предназначен для расчета и исследования линейных систем с постоянными параметрами.

При реализации этого пакета использованы принципы объектно-ориентированного программирования. Для линейных стационарных систем введен класс так называемых lti-объектов (linear time invariant object – линейные инвариантные во времени объекты). Этот класс включает в себя три подкласса: подкласс ss– для описания объектов в пространстве состояний и подклассы tf и zpk – для представления объектов в виде передаточных функций (ПФ).

Модель системы, заданная в одном из этих подклассов, может быть преобразована в любой другой подкласс. Дополнительные параметры позволяют указать, является ли система непрерывной или дискретной, имеется ли запаздывание на входах системы, задать наименования входов, выходов, переменных состояния, а так же другую вспомогательную информацию о системе.

Формирование tf-объектов

Математическая модель непрерывной системы в форме tf-объекта (transfer function - передаточная функция) имеет следующий вид:

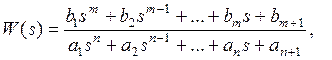(1.1)

где b_i , a_i – коэффициенты операторных полиномов соответственно числителя и знаменателя ПФ; s – комплексная переменная; m, n – соответственно порядки числителя и знаменателя ПФ.

Для создания (ввода) tf-модели используется функция с одноименным идентификатором:

,

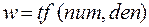где num = [b₁, b₂, …, b_m+1], den = [a₁, a₂, …, a_n+1] – соответственно массивы коэффициентов числителя и знаменателя ПФ вида (1.1); w – имя созданного объекта (передаточной функции) подкласса tf.

По умолчанию сформированные ПФ выводятся на экран в функции переменной s.

Пример 1.1. Создание объекта w₁ подкласса tf по передаточной функции вида

.

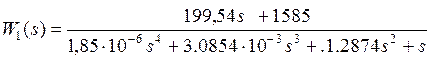Сравнивая с формой (1.1), получим

b₁=199,54, b₂=1585;

a₁=1,85 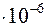, a₂=3,0854 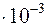, a₃=1,2874, a₄=1, a₅= 0.

В строке ввода команд набирается команда

>>w1=tf([199.54, 1585],[1.85e-6, 3.0854e-3, 1.2874, 1, 0])

Результат отобразится в следующей форме:

Transfer function:

199.5 s + 1585

1.85e-006 s^4 + 0.003085 s^3 + 1.287 s^2 + s

Задание 1.1. Сформируйте модель h1 tf-подкласса по ПФ вида

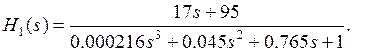
Для создания модели статического звена можно использовать команду tf(b₁, a₁) или tf(k), где k – коэффициент передачи.

Пример 1.2. Формирование модели электронного усилителя с коэффициентом передачи W(s)=150.

>> w2=tf(150)

Transfer function:

Задание 1.2. Создайте tf-модель h2 для безынерционного объекта с ПФ H₂(s)=11,45.