Момент сил относительно центра.

Необходимо ввести важное понятие о моменте силы относительно точки. Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки – моментом относительно центра. Если под действием силы тело может совершать вращение вокруг некоторой точки, то момент силы относительно этой точки будет характеризовать вращательный эффект силы.

Пусть в точке А твердого тела приложена сила (рис.1.7).Моментом силы относительно некоторого выбранного центра О называется векторная величина, обозначаемая и определяемая формулой:

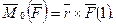, (1.2.1)

где 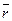-радиус-вектор точки А, .

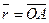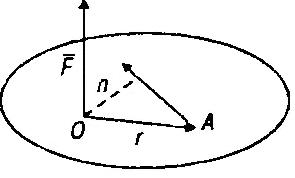
Рисунок 1.2.4

Из формулы (1.2.1) следует, что 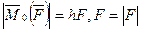где h - кратчайшее расстояние от точки О до линии действия силы, называемое плечом силы.

Вектор 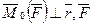и направлен в ту сторону, откуда вращение производимой силой видится происходящим против часовой стрелки. Если сила измеряется в [Н], то момент силы в [Н х м].

Отметим следующие свойства момента силы:

- момент силы относительно центра не изменяется при переносе точки приложения силы вдоль оси ее действия;

- момент силы относительно центра О равен нулю или когда сила равна нулю, или когда линия действия силы проходит через центр О (плечо равно нулю).

Теория пар сил.

Парой сил называют систему двух равных по модулю параллельных сил, направленных в противо­положные стороны. Известно, что под действием пары сил свободное твердое тело выходит из равновесия. Обычно пару сил прилагают к телу 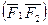, кото­рое должно вращаться. Поэтому пару сил нельзя заменить одной силой, и, следовательно, она не имеет равнодействующей. Такие силы имеют свойства обычных сил. Плоскостью действия пары сил N называют плоскость, в которой расположе­ны пары сил. Плечом пары h называется кратчайшее расстояние между линиями действия сил пары.

Алгебраическим моментом пары сил называют взятое со знаком плюс или минус произ­ведение одной из сил пары на плечо пары сил, т. е. 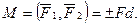Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится вращать тело по часовой стрел­ке. Алгебраический момент пары сил не зависит от переноса сил пары вдоль своих линий действия и может быть равен нулю, если линии действия пары сил совпадают, т. е. в случае двух равных по модулю, но противоположных по направлению сил, действующих вдоль прямой. Алгебраическим моментом пары относительно точки называют произведе­ние модуля силы на плечо силы относительно этой точки 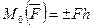. Плечом пары h относительно точки называется кратчайшее расстояние между этой точкой и линией действия силы, т. е. длина отрезка перпендикуляра, опущенного из точки на линию дей­ствия силы. Две пары сил называют эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях, если они имеют одинаковые по модулю и направлению векторные моменты.

Теорема об эквивалентности пары сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алгебраический момент.Иначе: две пары сил, рас­положенные в одной плоскости, эквивалентны, если они имеют одинаковые алгебраические моменты.

Выводы:

1) пару сил как жесткую построенный на фигуру можно как угодно пово­рачивать и переносить в ее плоскости действия;

2) у пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия.

Эти операции над парами сил не изме­няют их действия на твердое тело.

Теорема о сумме алгебраических моментов пары сил. Пары сил, действующие на твердое тело и расположенные в одной плоскости, можно привести к одной паре сил, алгебраический момент которой равен сумме алгебраических моментов составляющих пар сил, т. е. 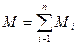Так же складываются пары сил, расположенные параллельных плоскостях, так как их предварительно можно перенести в одну плоскость.