Графический способ определения равнодействующей сходящихся сил на плоскости.

Пусть задана произвольная система сходящихся сил 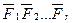, приложенных к твердому телу.

Перенесем эти силы как скользящие векторы в точку пересечения линий их действия. Затем, пользуясь аксиомой о параллелограмме сил, найдем равнодействую­щую этих сил. Равнодействующая такой системы может быть определена графически и аналитически.

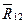Графически сложение двух сходящихся сил производится по правилу параллелограмма, причем . Затем по правилу параллелограмма складываем силы и 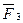, и получаем их равнодействующую 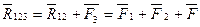. Продолжая процесс, получим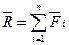

Процесс последовательного применения правила параллелограмма приводит к построению многоугольника из заданных сил. В силовом мно­гоугольнике конец одной из сил служит началом другой. Равнодействующая сила 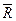в силовом многоугольнике соединяет начало первой силы с концом последней, т.е. изображается замыкающей силового многоугольника.

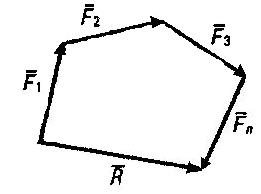
Рисунок 1.2.3.

Для пространственной системы сходящихся сил силовой многоугольник является пространственной фигурой, для плоской - плоской.

Для равновесия системы сходящихся сил, приложенных к твердому телу, замыкающая силового многоугольника, изображающая равнодействующую силу, должна обратиться в точку, т. е. конец последней силы в многоугольнике должен совпадать с началом первой силы.

Такой силовой многоугольник называют замкнутым.

Получено условие равновесия системы сходящихся сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сила равнялась нулю 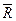= 0. Это условие является геометрическим.

Для случая трех сходящихся сил при равновесии должен быть замкнутым силовой треугольник, построенный из трех сил.