Магнитная индукция и напряженность на первом участке сердечника

В₁ = 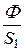= = 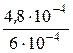0,8 Тл, Н₁= 1,15 А/см.

Намагничивающая сила, необходимая для создания потока Ф = = 4,8×10^-4 Вб определяется законом полного тока

IW = H₁×l₁+ H₂×l₂+H_В×l_В= 1,15×20 + 4,65×40 + 0,96×10⁴×0,12 = 1241 А,

что меньше заданного значения IW = 5×500 = 2500 А.

Для второго шага приближения необходимо увеличить значение В₂.

Результаты расчётов на каждом шаге сведём в табл. 2.22. Методом линейной интерполяции интервала двух последних шагов получаем значение В₂для заданной МДС F = 2500 A: В₂= В_В = 1,514 Тл,

а остальной расчёт отображает последняя колонка приведенной табл. 2.22, данные которой можно принять за результаты окончательного расчёта. При этом относительная погрешность расчёта по намагничивающей силе

d % = 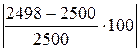= 0,1%.

Таблица 2.22

В₂=В_В, Тл	1,2	1,4	1,5	1,55	1,514
Н₂, А/см	4,65				0,508
Н_В, ´10⁴ А/см	0,96	1,12	1,2	1,24	1,211
Ф, ´10^–4 Вб	4,8	5,6		6,2	6,056
В₁, Тл	0,8	0,933		1,033	1,01
Н₁, А/см	1,15	1,67		2,33	2,1
SН×l, А

Запас энергии участка магнитной цепи W_м = 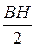×S×l=½Ф×U_м.

Для участков цепи: W_м₁ = ½×6,056×10^-4×2,1×20 = 127,2×10^-4 Дж;

W_м₂ = ½×6,056×10^-4×25,08×40 = 3038×10^-4 Дж;

W_мВ = ½×6,056×10^-4×1,211×10⁴×0,12 = 4040×10^-4 Дж.

Суммарный запас энергии магнитного поля исследуемой цепи

W_м = W_м₁+ W_м₂ + W_мВ = 7565×10^-4 Дж.

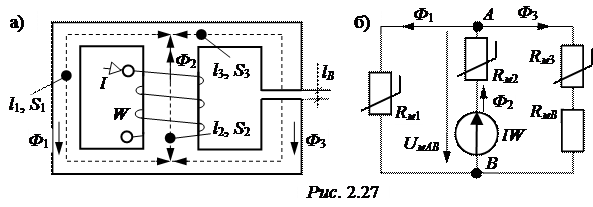
ЗАДАЧА2.23. Сердечник разветвлённой магнитной цепи рис. 2.27,а выполнен из электротехнической стали 1512. Размеры сердечника l₁= 60 см, S₁= 6 см², l₂= 20 см, S₂= 12 см², l₃= 40 см, S₃= S_В = 8 см², l_В = 1 мм. Число витков катушки W = 400. В воздушном зазоре требуется создать магнитное поле интенсивности В_В = 1,1 Тл. Найти ток катушки.

Решение

Для удобства расчётов приведём схему замещения магнитной цепи (рис. 2.27,б).

Магнитный поток Ф₃ = В_В×Н_В = 1,1×8×10^-4 = 8,8×10^-4 Вб,

магнитное напряжение U_мАВ = Н₃×l₃ + Н_В×l_В.

По кривой намагничивания при В₃= В_В = 1,1 Тл Н₃= 3 А/см,

Н_В = 0,8×10⁴×В_В = 0,8×10⁴×1,1 = 0,88×10⁴ А/см,

U_мАВ = 3×40 + 0,88×10⁴×0,1 = 1000 А.

Напряжённость магнитного поля параллельно включенной ветви

Н₁ = 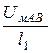= = 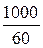16,7 А/см,

магнитная индукция в соответствии с кривой намагничивания В₁ = 1,462 Тл,

магнитный поток первого стержня Ф₁ = В₁×S₁= 1,462×6×10^-4 = 8,77×10^-4 Вб.

Магнитный поток среднего стержня

Ф₂ = Ф₁+ Ф₃= (8,77+8,8)×10^-4 = 17,57×10^-4 Вб,

магнитная индукция В₂ = 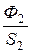= = 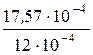1,464 Тл,

соответствующая напряжённость поля Н₂ = 16,96 А/см.

По закону полного тока IW = H₂×l₂+U_мАВ,

откуда I = 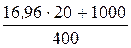=3,35 А.

ЗАДАЧА 2.24. В условиях задачи 2.23 вместо В_В задан поток Ф₁= = 8,4×10^-4 Вб. Найти намагничивающую силу.

Ответ: IW =844 А.

ЗАДАЧА 2.25. В условиях задачи 2.23 вместо В_Взадан поток Ф₂= = 18,6×10^-4 Вб. Определить намагничивающую силу.

Указание. При решении задачи рекомендуется рассчитать результирующую веберамперную характеристику параллельно включенных ветвей №1 и №3.

Ответ: IW =1710 А.

ЗАДАЧА 2.26. Магнитная цепь рис. 2.28,а выполнена из стали 1512 и имеет следующие размеры: l₁= 40 см, l₂= 12 см, l₃= 30 см, S₁= S₃= 4 см², S₂= 2 см². Намагничивающая сила IW = 1800 А, поток в первом стержне Ф₁= 5,8×10^-4 Вб. Определить длину воздушного зазора l_В.

Решение

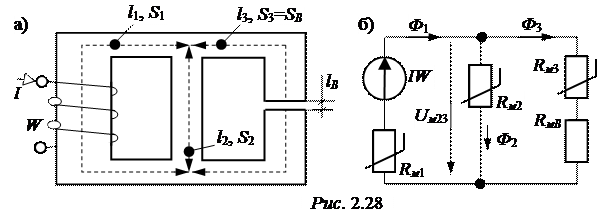Схема магнитной цепи соответствует смешанному соединению ветвей (рис. 2.28,б). На основании II закона Кирхгофа U_м₂₃= IW – Н₁×l₁.

Для определения Н₁по кривой намагничивания требуется найти

В₁ = 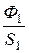= = 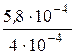1,45 Тл,

чему соответствует Н₁= 15 А/см, а U_м₂₃= 1800 – 15×40 = 1200 А.

С другой стороны, U_м₂₃= Н₂×l₂, откуда

Н₂ = 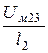= = 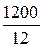100 А/см,

и на основании кривой намагничивания получаем В₂= 1,66 Тл.

Поток Ф₂ = В₂×S₂= 1,66×2×10^-4 = 3,32×10^-4 Вб.

На основании I закона Кирхгофа

Ф₃ = Ф₁– Ф₂= (5,8 – 3,32)×10^-4 = 2,48×10^-4 Вб,

а индукция В₃ = В_В = 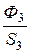= = 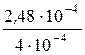0,62 Тл,

которой соответствует напряжённость магнитного поля в третьем стержне

Н₃ = 0,83 А/см,

а в воздушном зазоре Н_В = 0,8×10⁴×В_В = 0,8×10⁴×0,62 = 4960 А/см.

Падение магнитного напряжения на магнитном сопротивлении воздушного зазора Н_В×l_В = U_м₂₃– Н₃×l₃ = 1200 – 0,83×30 = 1175 А,

откуда искомая длина воздушного зазора l_В = 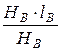= = 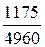0,237 см.

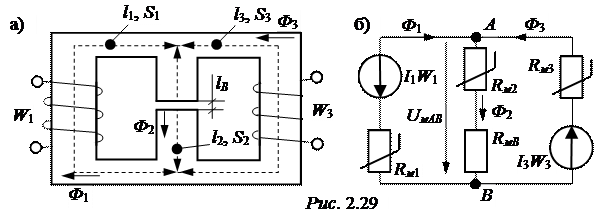ЗАДАЧА 2.27. Магнитная цепь, изображённая на рис. 2.29,а, выполнена из электротехнической стали 1512 и имеет следующие размеры: l₁= 60 см, l₂= 20 см, l₃= 80 см, l_В = 0,1 см, S₁= S₂= S₃= 10 см². Магнитные потоки в крайних стержнях Ф₁ = 0,25 мВб, Ф₃ = 1,3 мВб. Найти величины намагничивающих сил катушек, указать направления токов в обмотках.

Указание. При решении задачи удобно воспользоваться схемой замещения рис. 2.29,б с указанием произвольных направлений искомых намагничивающих сил, например, I₁W₁ вниз, I₃W₃вверх.

Ответы: I₁W₁= -1920 А, I₃W₃= 2490 А.

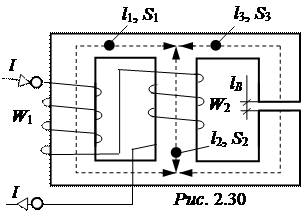
ЗАДАЧА2.28. Сердечник

разветвлённой магнитной цепи

(рис. 2.30) изготовлен из электротех-

нической стали 1512. По обмоткам

проходит ток I = 10 А, числа витков

W₁= 50, W₂= 35, размеры l₁= l₃= 30 см, l₂= 12 см, l_В = 0,1 см, S₁= S₂= S₃= = S_В= 15 см².

Определить магнитные потоки.

Ответы: Ф₁= 1,5 мВб, Ф₂= 0,7 мВб, Ф₃= 0,8 мВб.

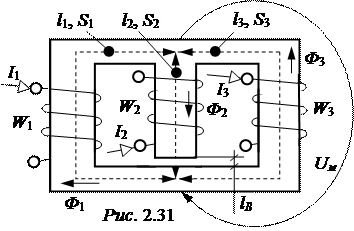ЗАДАЧА 2.29. Сердечник магнитной цепи (рис. 2.31) изготовлен из электротехнической стали 1512, кривая намагничивания которой приведена в задаче 2.18. Размеры сердечника l₁= l₃= 33 см, l₂= 11 см, l_В = 0,1 см, S₁= =12 см², S₂= 24 см², S₃= 16 см². Намагничивающие силы I₁W₁= 500 А, I₂W₂= =1000 А, I₃W₃= 750 А.

Определить магнитные потоки всех участков.

Решение

Выбираем произвольные направления магнитных потоков и узлового напряжения и составляем уравнения по методу узлового напряжения:

U_м = I₁W₁– Н₁×l₁,

U_м = -I₂W₂ + Н₂×l₂ + Н_В×l_В,

U_м = I₃W₃ – Н₃×l₃.

Расчёт зависимостей потоков от узлового напряжения сведём в таблицу (табл. 2.23):

Таблица 2.23

В	Н	Н_В	Н₁×l₁= =Н₃×l₃	Ф₁	U_м = I₁W₁ –– Н₁×l₁	Ф₂	U_м= -I₂W₂ + Н₂×l₂ + + Н_В×l_В	Ф₃	U_м = I₃W₃ –– Н₃×l₃
Тл	А/см	´10³ А/см	А	´10^-4 Вб	А	´10^-4 Вб	А	´10^-4 Вб	А
0,4	0,5	3,2	16,5	4,8		9,6	-674,5	6,4
0,8	1,15	6,4		9,6		19,2	-347	12,8
							-178
1,1		8,8		13,2		26,4	-87	17,6
1,2	4,65	9,6	153,5	14,4		28,8		19,2
1,3	7,4	10,4		15,6		31,2		20,8
1,4		11,2		16,8		33,6		22,4
1,45		11,6		17,4		34,8		23,2
1,5					-226
1,6		12,8		19,2	-1117	38,4		25,6	-867

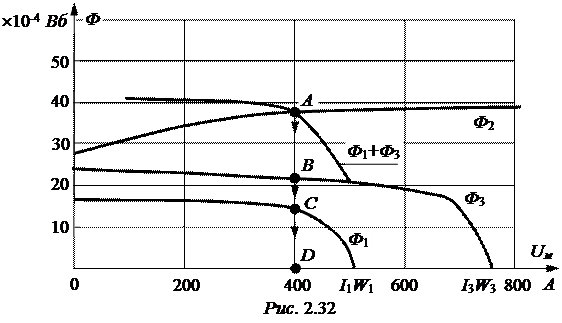
Графический расчёт магнитной цепи с учётом первого закона Кирхгофа Ф₁+ Ф₃= Ф₂при одном значении U_м приведен на рис. 2.32.

Точка пересечения А (Ф₁+Ф₃)(U_м) = Ф₂(U_м) определяет величину узлового напряжения U_м и поток Ф₂, а точки В и С – потоки Ф₁и Ф₃:

U_м= 400 А, Ф₂= 35,6×10^-4 Вб, Ф₁= 13,2×10^-4 Вб, Ф₃= 22,4×10^-4 Вб.

Напряжения на сопротивлениях ветвей:

U_м₁= Н₁×l₁= I₁W₁ - U_м= 500 – 400 = 100 А,

U_м₂ = Н₂×l₂ + Н_В×l_В= I₂W₂ + U_м= 1000 + 400 = 1400 А,

U_м₃= Н₃×l₃= I₃W₃ – U_м= 750 – 400 = 350 А.

Проверка баланса энергии:

S IW×Ф = (500×13,2+1000×35,6+750×22,4)×10^-4 = 5,9 Дж,

SU_м×Ф = (100×13,2+1400×35,6+350×22,4)×10^-4 = 5,9 Дж.

Так как S IW×Ф = SU_м×Ф, то задача решена верно.

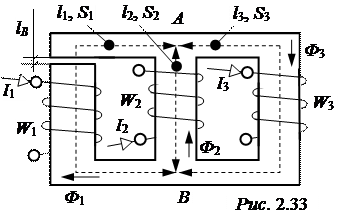
ЗАДАЧА 2.30. Магнитная цепь рис. 2.33 выполнена из элект-ротехнической стали 1512. Разме-ры сердечника l₁= l₃= 44 см, l₂= = 22 см, l_В = 0,4 мм, S₁= S₃=20 см², S₂= 10 см². Намагничивающие си-лы I₁W₁= 400 А, I₂W₂= 200 А, а потоки Ф₁= Ф₂.

Найти поток Ф₃и намагни-чивающую силу I₃W₃.

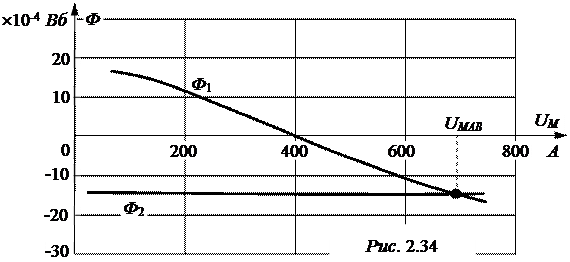
Методические указания к решению задачи. По методу двух узлов рекомендуется рассчитать и построить зависимости Ф₁(U_мАВ) и Ф₂(U_мАВ), точка их пересечения определит величину U_мАВ, а также Ф₁и Ф₂, затем с помощью второго закона Кирхгофа можно найти I₃W₃ (см. рис. 2.34).

U_мАВ = I₁W₁ – Н₁×l₁– Н_В×l_В, U_мАВ = -I₂W₂ – Н₂×l₂, I₃W₃ = U_мАВ – Н₃×l₃.

Ответы: Ф₁= Ф₂= -15,5×10^-4 Вб, U_мАВ = 690 А, Ф₃= -31×10^-4 Вб, I₃W₃ = 2140 А.

1 2 34

Дата добавления: 2016-01-18; просмотров: 1797;