Кривая намагничивания стали 1512
| В, Тл | 0,2 | 0,4 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 1,1 | |
| Н, А/см | 0,25 | 0,5 | 0,65 | 0,8 | 0,95 | 1,15 | 1,5 |
Продолжение таблицы 2.19
| В, Тл | 1,2 | 1,3 | 1,35 | 1,4 | 1,45 | 1,5 | 1,55 | 1,6 | 1,65 |
| Н, А/см | 4,65 | 7,4 |
 |
Решение
Вебер-амперная характеристика катушки Ф(I) рассчитывается на основании кривой намагничивания и геометрических размеров ферромагнитного сердечника: приняв, например, В = 1,2 Тл с соответству-ющим значением Н = 4,65 А/см, получаем
Ф = В×S = 1,2×16×10 –4 = 19,2×10 –4 Вб, I =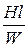 
= 
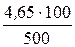= 0,93 А.
Результаты расчёта сведём в таблицу (табл. 2.20).
Таблица 2.20
| В, Тл | 0,4 | 0,6 | 0,8 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 | |
| Н, А/см | 0,5 | 0,8 | 1,15 | 4,65 | 7,4 | |||||
| Ф,´ 10 –4 Вб | 6,4 | 9,6 | 12,8 | 17,6 | 19,2 | 20,8 | 22,4 | 25,6 | ||
| I, А | 0,1 | 0,16 | 0,23 | 0,4 | 0,6 | 0,93 | 1,48 | 2,4 | 4,4 | 9,8 |
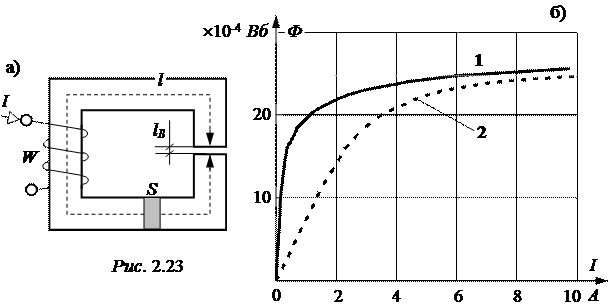
Вебер-амперная характеристика катушки без воздушного зазора приведена на рис. 2.23,б, кривая 1.
ЗАДАЧА 2.19. В сердечнике катушки задачи 2.18 выполнен воздушный зазор длиной lВ = 1,2 мм. Построить вебер-амперную характе-ристику катушки с воздушным зазором.
Решение
По сравнению с предыдущей задачей изменится ток катушки при прежних значениях потока, так как в соответствии с законом полного тока новое значение тока
I =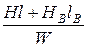 
.
Напряжённость магнитного поля в воздушном зазоре
НВ =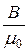 
= 
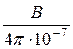= 0,8×106×В, где HВ[А/м], В[Тл]
или НВ = 0,8×104×В, где HВ[А/см], В[Тл].
Например, для индукции В = 1,2 Тл Н = 4,65 А/см,
НВ = 0,8×104×1,2 = 9,6×103 А/см,
новый ток
I = +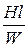 
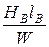= I¢ + I¢¢ = + 
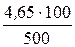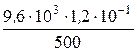= 0,93+2,304 = 3,324 А.
Веберамперная характеристика в табличной форме приобретает вид табл. 2.21.
Таблица 2.21
| Ф, ´10 –4 Вб | 6,4 | 9,6 | 12,8 | 17,6 | 19,2 | 20,8 | 22,4 | 25,6 | ||
| I, А | 0,87 | 1,31 | 1,77 | 2,32 | 2,71 | 3,32 | 3,98 | 5,09 | 7,28 | 12,9 |
Эта веберамперная характеристика приведена на рис. 2.23,б, кривая 2.
При расчётах магнитных цепей часто используют магнитное сопротивление участка магнитной цепи
Rм =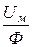 
= 
= 
= 
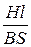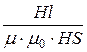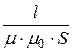[1/Гн].
Для приведенного примера магнитное сопротивление участка магнитопровода длиной l = 100 см, сечения S = 16 см2 при В = 1,2 Тл, Н = = 4,65 А/см
RмС = 
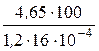= 24,22×104 1/Гн,
а сопротивление воздушного зазора длиной lВ = = 1,2 мм, сечения S = 16 см2 при В = 1,2 Тл
RмВ =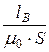 
= 
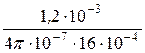=59,71×104 1/Гн.
Таким образом, при В = 1,2 Тл сопротивление воздушного зазора длиной 1,2 мм магнитному потоку больше сопротивления сердечника длиной 1 м в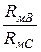 
= 
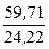= 2,5 раза.
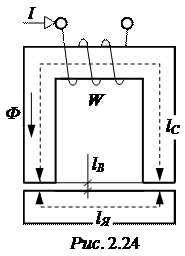
ЗАДАЧА 2.20. В воздушном зазоре электромагнита (рис. 2.24) требует-ся создать магнитное поле с магнитной индукцией В = 1,1 Тл. Сердечник и якорь выполнены из электротехнической стали 1512, кривая намагничивания которой приведена в задаче 2.18, имеют одинаковое сечение SС = SЯ = S = = 20 см2. Длина сердечника lС = 80 см, якоря – lЯ = 30 см. Число витков катушки W = 800. Длина одного воздушного зазора lВ = 0,4 мм. Определить:
- ток в обмотке катушки;
- индуктивность катушки;
- силу, с которой якорь притягивается к сердечнику;
- отрывную силу электромагнита.
Решение
По закону полного тока необходимая намагничивающая сила катушки
IW = HС×lС + HЯ×lЯ +2×HВ×lВ .
Магнитный поток катушки Ф = В×SВ .
Так как SВ = SС = S, то ВВ = ВС = В и по кривой намагничивания при В = 1,1 Тл НС = НЯ = 3 А/см,
НВ = 0,8×104×В = 0,8×104×1,1 = 8,8×103 А/см,
IW = 3×80 + 3×30 + 2×8,8×103×0,4×10-1 = 1034 А,
полный ток катушки I =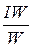 
= 
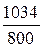= 1,29 А.
Потокосцепление катушки Y = В×S×W = 1,1×20×10-4×800 = 1,76 Вб,
индуктивность катушки L =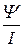 
= 
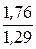= 1,36 Гн.
Силу тяги электромагнита на один воздушный зазор рассчитаем по методу возможных перемещений (см. курс «Прикладная механика»). Энергия магнитного поля в воздушном зазоре
WВ =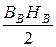 
VB = 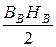×SВ×lВ.
При бесконечно малом перемещении якоря изменяется длина воздушного зазора при неизменных ВВ, НВ. Сила притяжения якоря к сердечнику на один воздушный зазор
F1 = -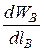 
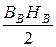= - ×SВ.
Дата добавления: 2016-01-18; просмотров: 2891;