МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ И МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Между величинами, характеризующими электрические и магнитные цепи, существует формальная аналогия:
| Электрические цепи | Магнитные цепи |
| Ток I, А | Поток Ф, Вб |
| ЭДС Е, В | МДС F=I×W, А |
| Сопротивление r, Ом | Магнитное сопротивление RM, 1/Гн |
| Напряжение U, В | Магнитное напряжение UM=H×l, А |
Эта формальная аналогия распространяется и на уравнения, описывающие состояние цепей:
- первый закон Кирхгофа: S I = 0, S Ф = 0;
- второй закон Кирхгофа: S Ur = S Е, S UМ = S F;
- закон Ома: Ur = I×r, UМ = Ф×RM ;
причём в последних выражениях используются статические сопротивления электрических элементов (r) и магнитных элементов (RM).
Свойства нелинейных элементов определяются их характеристиками: электрических – вольтамперными U = f(I), магнитных – вебер-амперными Ф = f(UM).
Системы уравнений, описывающих состояние цепей, составляются с помощью законов Кирхгофа. С точки зрения математики – это нелинейные алгебраические уравнения, для разрешения которых применяются различные приближённые методы, которые в курсе ТОЭ называют методами расчёта нелинейных цепей.
Наиболее часто употребляются:
1) графические методы;
2) графо-аналитические методы;
3) численные методы.
НЕЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ
Свойства нелинейных элементов определяются их вольтамперными характеристиками и в рассматриваемых задачах анализа электрических цепей считаются заданными: либо снятыми экспериментально с помощью вольтметров и амперметров, либо определяются паспортными данными по каталогам или данным заводов-изготовителей.
ЗАДАЧА 2.1. На рис. 2.1,а приведена вольтамперная характеристика лампы накаливания с вольфрамовой нитью, на рис. 2.1,б – стабилитрона, на рис. 2.1,в – туннельного диода. Для указанных точек (рабочих точек устройства, точек равновесия) определить статические и дифференциальные сопротивления элементов.
Решение
Проведём через указанные точки секущие из начала координат (сек) и касательные (кас). Для рис. 2.1,а получаем:
rстА = 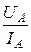 =
= 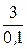 = 30 Ом, rдА =
= 30 Ом, rдА = 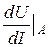 = lim
= lim 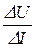 =
= 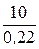 = 45,5 Ом;
= 45,5 Ом;
rстВ = 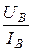 =
= 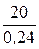 = 83,3 Ом, rдВ =
= 83,3 Ом, rдВ = 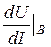 =
= 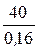 = 250 Ом;
= 250 Ом;
rстС = 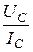 =
= 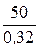 = 156,3 Ом, rдС =
= 156,3 Ом, rдС = 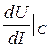 =
= 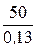 = 385 Ом.
= 385 Ом.
Для рис. 2.1,б получаем:
rстА = 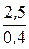 = 6,25 Ом, rдА =
= 6,25 Ом, rдА = 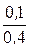 = 0,25 Ом;
= 0,25 Ом;
rстВ = 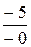 = ¥ Ом, rдВ =
= ¥ Ом, rдВ = 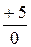 = ¥ Ом;
= ¥ Ом;
rстС = 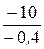 = 25 Ом, rдС =
= 25 Ом, rдС = 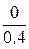 = 0 Ом.
= 0 Ом.
Для рис. 2.1,в получаем:
rстА = 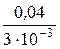 = 13,3 Ом, rдА =
= 13,3 Ом, rдА = 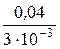 = 13,3 Ом >0;
= 13,3 Ом >0;
rстВ = 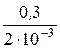 = 150 Ом, rдВ =
= 150 Ом, rдВ = 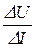 =
= 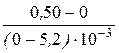 = -96,2 Ом < 0;
= -96,2 Ом < 0;
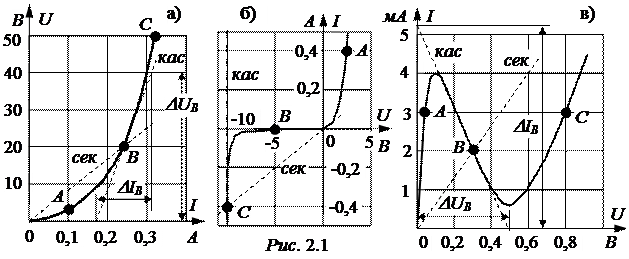 |
rстС =
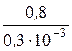 = 267 Ом, rдС =
= 267 Ом, rдС = 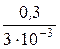 = 100 Ом > 0.
= 100 Ом > 0.
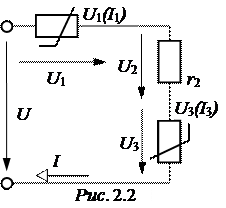
Заметим, что на спадающем участке вольтамперной характеристики дифференциаль-ное сопротивление отрицательное.
ЗАДАЧА 2.2. Рассчитать ток цепи рис.2.2, проверить баланс мощностей, если U = 100 В, r2 = 20 Ом, вольтамперные характеристики нелинейных резисторов заданы таблицами:
Таблица 2.1 Таблица 2.2
| U1, В | U3, В | |||||||||||
| I1, A | 0,5 | I3, A |
Решение
Воспользуемся графическим методом расчёта нелинейной электрической цепи, предварительно составив систему расчётных уравнений:
по второму закону Кирхгофа U1 + U2 + U3 = U,
причём из-за последовательного соединения резисторов их токи одинаковы:
I1 = I2 = I3 = I,
связи между токами и напряжениями участков с нелинейными элементами
U1= f1(I1) – таблица 1, U3= f2(I3) – таблица 2,
а для линейного элемента по закону Ома имеем аналитическую зависимость
U2 = I2×r2.
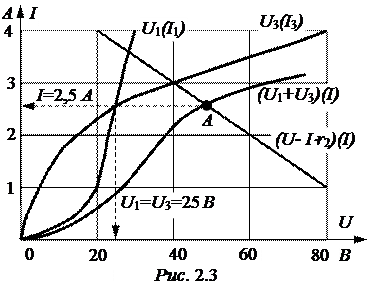
Графические построения, соответствующие приведенной системе уравнений, показаны на рис. 2.3 и выполнены в системе прямоугольных координат I(U).
Перепишем исходное уравнение, записанное по второму закону Кирхгофа, оставив в левой части напряжения на нелинейных элементах, а в правую часть перенесём линейное соотношение U2 = I×r2:
 U1 + U3 = U – I×r2.
U1 + U3 = U – I×r2.
Построим вспомогатель-ные зависимости (рис. 2.3)
(U1 + U3)(I) и (U – I×r2)(I),
точка пересечения А которых определяет решение задачи:
I = 2,5 А, U1 = 25 В, U3 = 25 В.
Проверка баланса мощ-ностей:
- мощность источника питания (генератора)
РГ = U×I = 100×2,5 = 250 Вт;
- сумма потребляемых резисторами мощностей
SРП = U1×I + U3×I + I 2×r2 = 25×2,5 +25×2,5 + 2,52×20 = 250 Вт.
Баланс мощностей РГ =SРП сходится, задача решена верно.
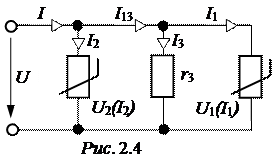
ЗАДАЧА 2.3. Графическим методом рассчитать токи в схеме рис. 2.4 и напряжение источника питания, проверить баланс мощностей, если
I13 = 5 А, r3 = 14 Ом,
вольтамперные характеристики нелиней-ных резисторов заданы таблицами:
Таблица 2.3 Таблица 2.4
| U1, В | U2, В | ||||||||||||
| I1, A | 4,8 | I2, A | 1,25 | 2,5 | 3,3 |
Решение
Для параллельного соединения исходные уравнения запишем по первому закону Кирхгофа, к которым добавим уравнения связей между токами и напряжениями участков: I13 = I1 + I3, I = I2 + I13,
I1 = f1(U1), I2 = f2(U2), U3 = I3×r3, причём U = U1 = U2 = U3.
Решим сначала первое из приведенных уравнений, переписав его в виде I1 = I13 - 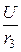 ,
,
где слева – ток нелинейного элемента I1 = f1(U),задан табл. 2.3, а справа – линейная зависимость от напряжения U: I13 - 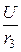 = 5 -
= 5 - 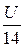 .
.
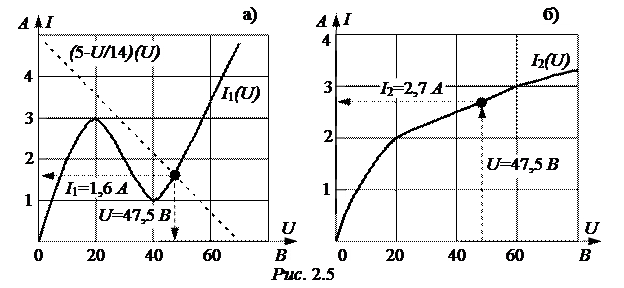 |
Указанные зависимости приведены на рис. 2.5,а вместе с решением первого из приведенных уравнений.
Так как графический расчёт имеет значительную погрешность, выполним проверку решения по рис. 2.5,а: равно ли I1 = I13 - 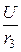 ?
?
1,6 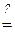 (5 –
(5 – 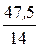 ) = (5 – 3,393) = 1,607, где I3 = 3,393 А.
) = (5 – 3,393) = 1,607, где I3 = 3,393 А.
Результат отличается в 4м знаке, что указывает на достаточную точность решения.
На рис. 2.5,б показано определение тока I2.
Ток генератора I = I2 + I13 = 2,7 + 5 = 7,7 А.
Мощность генератора РГ = U×I = 47,5×7,7 = 365,8 Вт;
Сумма мощностей потребителей
SРП = U×I2 + I32×r3 + U×I1 = 47,5×2,7 + 3,3932×14 + 47,5×1,6 = 365,4 Вт.
РГ » SРП – выполняется.
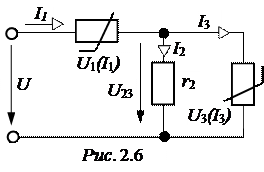 ЗАДАЧА2.4. Рассчитать токи, проверить баланс мощностей в схеме рис. 2.6, если U = 80 В, r2 = 10 Ом, вольтамперные характеристики нелинейных резисторов заданы таблицами:
ЗАДАЧА2.4. Рассчитать токи, проверить баланс мощностей в схеме рис. 2.6, если U = 80 В, r2 = 10 Ом, вольтамперные характеристики нелинейных резисторов заданы таблицами:
Таблица 2.5
| U1, В | ||||||
| I1, A |
Таблица 2.6
| U3, В | ||||||
| I3, A | 5,2 | 6,5 |
Решение
В системе координат U(I) рис. 2.7 строим вольтамперные характеристики параллельно включенных элементов I3(U3) и U2 = I2×r2, а также вспомогательную характеристику
(I2+ I3)(U23) = (I1)(U23), так как I1= (I2+ I3).
По второму закону Кирхгофа U1+U23= U или U23= U – U1.
Строим вспомогательную характеристику U – U1 = U – f1(I1),
которую рассчитываем,задаваясь рядом значений тока I1. Результаты расчёта сводим в табл. 2.7.
Таблица 2.7
| I1, А | |||||||
| U1, В | |||||||
| U – U1= 80 – U1, В |
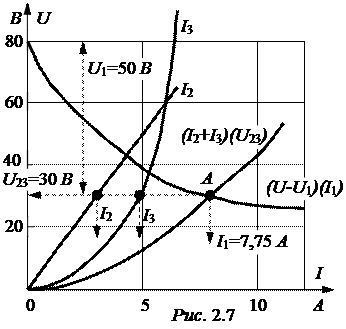 Точка А пересечения двух вспомогательных кривых опреде-ляяет решение задачи: I1= 7,75 А, U23= 30 В, I2= 3 А, I3= 4,75 А, U1= 50 В.
Точка А пересечения двух вспомогательных кривых опреде-ляяет решение задачи: I1= 7,75 А, U23= 30 В, I2= 3 А, I3= 4,75 А, U1= 50 В.
Проверка баланса мощнос-тей: РГ = U×I1 = 80×7,75 = 625 Вт;
SРП = U1×I1 + I22×r2 + U23×I3 =
= 50×7,75+32×10+30×4,75 = 620 Вт.
ЗАДАЧА 2.5. Две электри-ческие лампы накаливания с номинальным напряжением 127 В каждая и мощностью 40 и 70 Вт включены последовательно в сеть с напряжением U = 240 В. По предварительному расчёту (сопротивления ламп неизменны) напряжения на лампах U1= 152,5 В, U2 = 87,5 В. В действительности вольтамперные характеристики ламп нелинейны и заданы табл. 2.8.
Таблица 2.8
| U, В | ||||||||||
| I1, А | 0,16 | 0,2 | 0,24 | 0,27 | 0,3 | 0,33 | 0,35 | 0,38 | 0,41 | 0,43 |
| I2, А | 0,32 | 0,38 | 0,44 | 0,49 | 0,54 | 0,58 | 0,63 | 0,68 | 0,73 | 0,78 |
 Определить напряжения на лампах.
Определить напряжения на лампах.
Ответ: U1= 180 В, U2= 60 В.
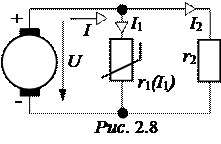
ЗАДАЧА 2.6. Внешняя характеристика генератора постоянного тока (рис.2.8) опреде-ляется данными табл. 2.9.
Таблица 2.9
| U, В | |||||||||||
| I, А |
Нелинейный элемент r1(I1) характеризуется вольтамперной характеристикой табл. 2.10.
Таблица 2.10
| U1, В | |||||||
| I1, А |
Сопротивление r2 = 6 Ом. Определить токи во всех ветвях схемы
рис. 2.8.
Ответы: I1 = 86 А, I2 = 24 А, I = 110 А.
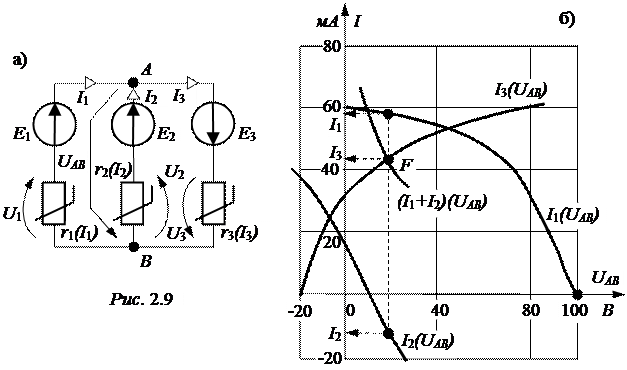
ЗАДАЧА 2.7. На рис. 2.9,а изображена схема с тремя одинаковыми нелинейными элементами, вольтамперные характеристики которых заданы табл. 2.11. ЭДС источников напряжения Е1 = 100 В, Е2 = 10 В, Е3 = 20 В. Определить токи во всех ветвях схемы, пренебрегая внутренними сопротивлениями источников.
Таблица 2.11
| ±U, В | |||||||
| ±I, мА |
Решение
Так как все ветви схемы подключены параллельно к двум узлам схемы А и В, для решения задачи воспользуемся методом узлового напряжения, выбрав произвольные направления токов в ветвях и узлового напряжения UАВ (указаны на схеме).
Для контуров, в каждый из которых входит UАВ и одна из ветвей, в соответствии со вторым законом Кирхгофа получаются три уравнения:
UАВ + U1 = Е1, UАВ + U2 = Е2, UАВ – U3 = -Е3.
Из этих уравнений выразим UАВ:
UАВ = Е1 – U1, UАВ = Е2 – U2, UАВ = -Е3 + U3.
На основании последних выражений удобно рассчитывается зависимость тока отдельной ветви от узлового напряжения в такой последовательности:
- задаёмся произвольным значением тока ветви в соответствии с вольтамперной характеристикой нелинейного элемента и определяем соответствующее этому значению напряжение нелинейного элемента;
- напряжение UАВ, при котором в ветви будет выбранное значение тока, рассчитываем по соответствующему уравнению второго закона Кирхгофа.
Рассчитанные зависимости I1(UАВ), I2(UАВ), I3(UАВ) приведены на рис. 2.9,б.
По первому закону Кирхгофа можно записать уравнение I1 + I2 = I3, которое для рассматриваемой схемы должно выполняться при одном значении UАВ. Построим вспомогательную кривую (I1+I2)(UАВ) и найдём точку F пересечения этой кривой с зависимостью I3(UАВ).
Точка F определяет решение задачи:
UАВ = 18 В, I1 = 58 мА, I2 = -15 мА, I3 = 43 мА,
напряжения на элементах U1= 82 В, U2= -8 В, U3= 38 В.
Алгебраическая сумма мощностей генераторов
SРГ = Е1×I1 + Е2×I2 + Е3×I3 = 100×58+10×(-15)+20×43 = 6510 мВт;
Сумма мощностей потребителей энергии
SРП = U1×I1 + U2×I2 + U3×I3 = 82×58 + (-8)×(-15) + 38×43 = 6510 мВт.
 Баланс мощностей выполняется.
Баланс мощностей выполняется.
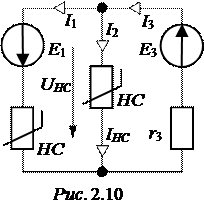
ЗАДАЧА 2.8. В схеме рис. 2.10 определить токи ветвей и проверить баланс мощностей, если Е1 = 120 В, Е3 = 20 В, r3 = 2 кОм, вольтамперная характеристика одинаковых нелинейных сопротивлений (НС) представлена в табл. 2.12.
Таблица 2.12
| UНС, В | |||||||
| IНС, мА |
Ответы: I1 = 58 мА, I2 = -35 мА,
 I3 = 23 мА, SР = 7420 мВт.
I3 = 23 мА, SР = 7420 мВт.
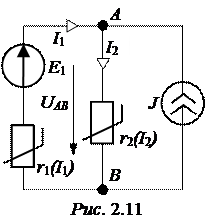
ЗАДАЧА 2.9. Вольтамперные характерис-тики нелинейных элементов r1(I1) и r2(I2), вклю-ченных в цепь рис. 2.11, приведены в табл. 2.13.
Таблица 2.13
| U, В | ||||||||
| I1, А | 0,2 | 0,4 | 0,68 | 0,86 | 0,96 | |||
| I2, А | 1,12 | 1,4 | 1,8 | 2,14 | 2,44 | 2,77 | 3,5 | - |
Найти токи, проверить баланс мощностей, если Е1 = 70 В, J = 1,5 А.
Ответы: I1 = 0,9 А, I2 = 2,4 А, UАВ = 38 В, SР = 120 Вт.
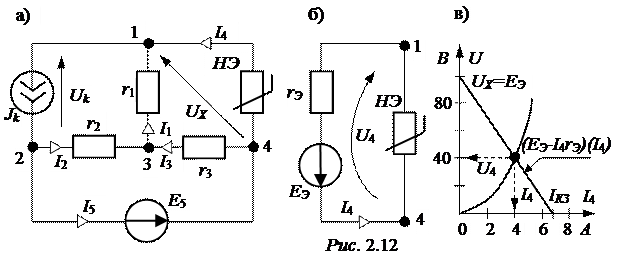
ЗАДАЧА 2.10. На рис. 2.12,а изображена схема с нелинейным элементом (НЭ), вольтамперная характеристика которого задана табл. 2.14.
Таблица 2.14
| U4, В | ||||||
| I4, А | 2,8 | 4,9 | 5,4 | 5,7 |
Параметры линейных элементов r1= r2= r3= 10 Ом, Е5 = 50 В, Jk = 5 А.
Определить токи во всех ветвях схемы и проверить баланс мощностей.
Решение
Сначала рассчитаем ток I4 нелинейного элемента, заменив линейную часть схемы по отношению к зажимам нелинейного элемента (1-4) эквивалентным генератором.
При этом UХ = ЕЭ = I3Х×r3 + I1Х×r1, где токи с индексом Х (холостой ход) – это токи элементов схемы, которые получаются после размыкания ветви с нелинейным элементом. В полученной таким образом более простой схеме I1Х= Jk = 5 А, а по методу контурных токов
I3Х= 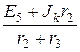 =
= 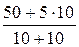 = 5 А,
= 5 А,
и UХ = 5×10 + 5×10 = 100 В.
 |
Внутреннее сопротивление эквивалентного генератора равно входному сопротивлению пассивной линейной схемы относительно зажимов 1-4:
rЭ = r14ВХ = r1 + 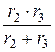 = 10 +
= 10 + 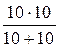 = 15 Ом.
= 15 Ом.
Для эквивалентной схемы (рис. 2.12,б), с одной стороны, U4(I4) – ВАХ НЭ, а с другой стороны, U4 = ЕЭ – I4×rЭ – ВАХ активного двухполюсника.
Решение системы двух последних уравнений представлено на рис. 2.12,в, откуда U4 = 40 В, I4= 4 А.
 Возвращаемся к исходной схеме рис. 2.12,а и рассчитываем остальные токи: I1= Jk - I4= 5 – 4 = 1 А,
Возвращаемся к исходной схеме рис. 2.12,а и рассчитываем остальные токи: I1= Jk - I4= 5 – 4 = 1 А,
I3= 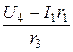 =
= 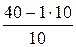 = 3 А,
= 3 А,
I5= I3 + I4= 3 + 4 = 7 А,
I2= I1 – I3= 1 - 3 = -2 А,
напряжение на зажимах источника тока
Uk = I2×r2 + I1×r1 = -2×10 +1×10 = -10 В.
Проверка баланса мощностей:
SРГ = Uk×Jk + Е5×I5 = -10×5+50×7 = 300 Вт;
SРП = I12×r1 + I22×r2 + I32×r3 + U4×I4 =
= 12×10 + 22×10 + 32×10 + 40×4 = 300 Вт.
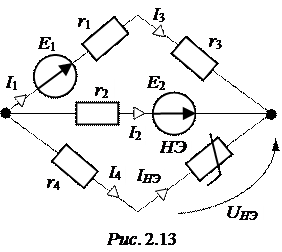
ЗАДАЧА 2.11. В схеме рис. 2.13 рассчитать все токи, если Е1 = 4 В,
Е2 = 16 В, r1 = r2 = r3 = 2 Ом, r4 = 4 Ом, вольтамперная характеристика НЭ представлена табл. 2.15.
Таблица 2.15
| UНЭ, В | |||||||
| IНЭ, А | 0,5 | 0,76 | 1,2 | 1,45 | 1,53 | 1,65 |
Ответы: I1 = I3 = -1,56 А, I2 = 2,88 А, I4 = IНЭ = -1,31 А.
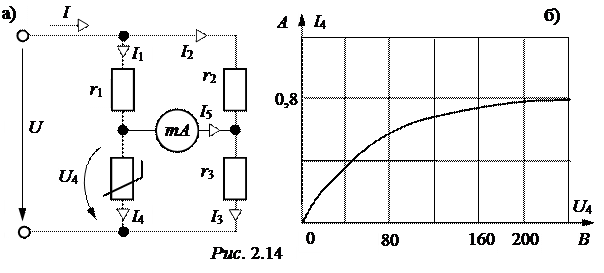 |
ЗАДАЧА 2.12. В схеме рис. 2.14,а определить токи и проверить баланс мощностей, если U = 240 В, r1= 240 Ом, r2= 400 Ом, r3= 600 Ом, сопротивление миллиамперметра mA – 160 Ом, вольтамперная характеристи-ка нелинейного элемента задана рис. 2.14,б.
|
I2 = 0,29 А, I3 = 0,2 А, I5 = -0,09 А,
SР= 204 Вт.
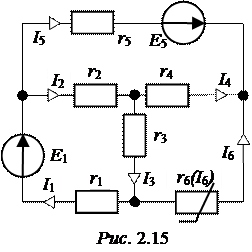
ЗАДАЧА 2.13. Определить токи, про-верить баланс мощностей, если Е1 = 160 В, Е5 = 180 В, сопротивления схемы рис. 2.15 r2 = r3= r4 = 10 Ом, r5= 30 Ом, r1= 40 Ом, вольтамперная характеристика нелинейного элемента в табл. 2.16.
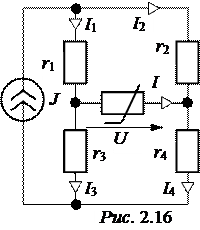 Таблица 2.16
Таблица 2.16
| U6, В | |||||||
| I6, А |
Ответы: I1 = 4 А, I2 = -1 А, I3 = 1 А,
I4 = -2 А, I5 = 5 А, I6 = -3 А,
U6 = -29,8 В, SР = 1540 Вт.
ЗАДАЧА 2.14. Определить токи в схеме рис. 2.16, проверить баланс мощностей, если
J = 0,4 А, r1= 4 Ом, r2= 6 Ом, r3= 24 Ом,
r4= 16 Ом, ВАХ U(I) приведена в табл. 2.17.
Таблица 2.17
| U, В | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,7 | 0,9 | 1,1 |
| I, мА |
Ответы: U = 0,37 В, I = 34 мА, I1 = 20,3 мА,
I2 =197 мА, I3 =169 мА, I4 = 231 мА, SР =1948мВт.
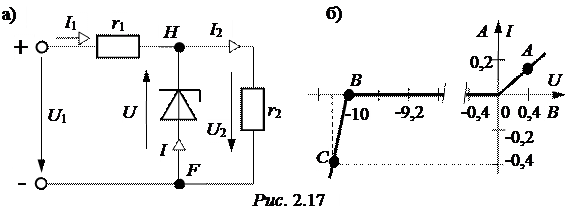 |
ЗАДАЧА 2.15. В схеме рис. 2.17,а r1= 10 Ом, r2= 20 Ом, напряжение U1 = 24 В, вольтамперная характеристика стабилитрона аппроксимирована тремя прямолинейными отрезками (рис. 2.17,б). Приведенная схема является простейшим стабилизатором напряжения U2 для нагрузки r2. Рассчитать токи и напряжение нагрузки в схеме, определить коэффициент стабилизации напряжения.
Решение
Определим дифференциальные сопротивления стабилитрона:
на участке ОА rд1= 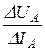 =
= 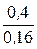 = 2,5 Ом;
= 2,5 Ом;
на участке ОВ rд2= ¥;
на участке ВС rд3= 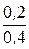 = 0,5 Ом.
= 0,5 Ом.
В рассматриваемой схеме напряжение на стабилитроне отрицательное и, если это напряжение меньше 10 В, ток стабилитрона I = 0. Тогда
I1 = I2 = 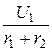 , U = -U2 = -
, U = -U2 = - 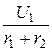 ×r2< -10 В = U0,
×r2< -10 В = U0,
откуда находим минимальное напряжение сети, при котором схема работает как стабилизатор напряжения:
U1min = -U0× 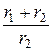 = -10×
= -10× 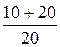 = 15 В.
= 15 В.
Так как заданное напряжение U1 = 24 В > U1min, то стабилитрон в схеме работает на участке ВС, его схемой замещения является цепочка рис. 2.18,а, а расчётная схема установки приведена на рис. 2.18,б. По методу узлового напряжения
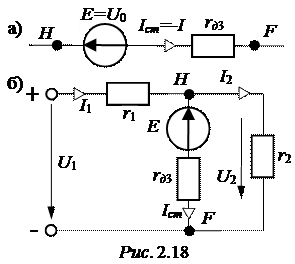 U2=
U2= 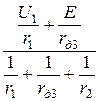 =
= 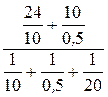 = 10,42 В.
= 10,42 В.
I1 = 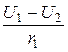 =
= 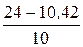 = 1,358 А,
= 1,358 А,
I2 = 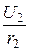 =
= 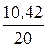 = 0,521 А,
= 0,521 А,
Iст = 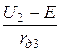 =
= 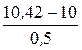 = 0,84 А.
= 0,84 А.
Пассивная схема стабилизатора рис. 2.17,а для приращений представлена на рис. 2.19, рассчитывая которую, получаем
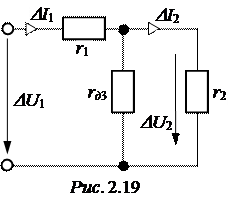 DU2 = DU1×
DU2 = DU1× 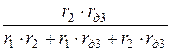 =
=
=DU1× 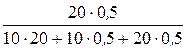 =DU1×0,0465.
=DU1×0,0465.
Коэффициент стабилизации стабилизатора напряжения
kст = 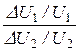 =
= 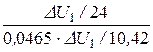 = 9,34.
= 9,34.
ЗАДАЧА 2.16. В четыре плеча моста, служащего стабилизатором напряжения (рис. 2.20), включены два НЭ1 и два НЭ2 так, что противоположные плечи моста одинаковы. Вольтамперные характеристики НЭ1 и НЭ2 могут быть аппроксимированы выражениями:
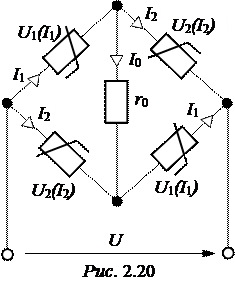 U1(I1) =400×I1 – 164, U2(I2) =400×I2 + 120,
U1(I1) =400×I1 – 164, U2(I2) =400×I2 + 120,
где U[В], I[мА].
Найти: 1) ток I0 в диагонали моста при сопротивлении нагрузки r0 = 285 Ом и напря-жении питания U = 140 В;
2) КПД моста (отношение мощности в диагонали моста к мощности источника) при U = 140 В;
3) положение рабочих точек на характеристиках при отклонении напряжения сети на DU = ±5%U (см. задачу 2.15);
4) коэффициент стабилизации стабили-затора напряжения (см. задачу 2.15).
Примечание: при решении по п.3 и п.4 рекомендуется воспользоваться схемой замещения стабилизатора для отклонений.
Ответы: I0 = 414 мА, h = 76%, kст = ¥.
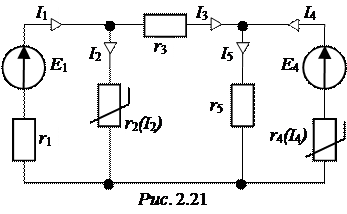 ЗАДАЧА2.17. В цепи рис. 2.21 кроме линейных сопротивлений
ЗАДАЧА2.17. В цепи рис. 2.21 кроме линейных сопротивлений
r1= 2 Ом, r3= 1 Ом, r5= 2 Ом
имеются ещё два одинаковых нелинейных резистора с заданной вольтамперной характеристикой (табл. 2.18).
Таблица 2.18
| U, В | |||||
| I, А | 0,2 | 0,5 | 1,0 | 2,0 |
ЭДС источников Е1 = 5 В, Е4 = 3 В. Найти токи во всех ветвях схемы.
Примечание: при решении задачи графическим методом рекомендуется одно из параллельных включений сначала заменить эквивалентной ветвью, а затем воспользоваться методом двух узлов.
Ответы: I1 = 1,3 А, I2 = 0,7 А, I3 = 0,6 А, I4 = 0,3 А, I5 = 0,9 А.
МАГНИТНЫЕ ЦЕПИ ПОСТОЯННОГО ТОКА
Отличительной чертой расчётов нелинейных магнитных цепей по сравнению с нелинейными электрическими является то, что в исходной задаче расчёта нет необходимых для расчёта вебер-амперных характеристик участков магнитной цепи.
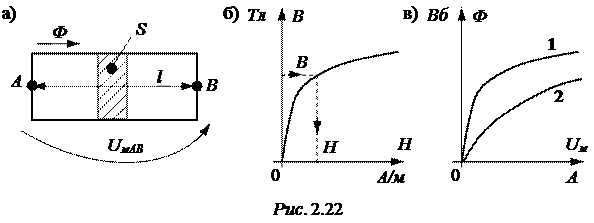 |
Участок (рис. 2.22,а) характеризуется длиной средней линии магнитопровода l, площадью поперечного сечения сердечника S, кривой намагничивания материала B(H) (рис. 2.22,б), а вебер-амперная характеристика Ф(I) (рис. 2.22,в) рассчитывается.
Магнитная индукция участка B = 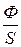 ,
,
где Ф[Вб] – магнитный поток, В[Тл].
Магнитное напряжение на участке UмАВ = H×l = Ф×Rм,
где H[А/м] – напряжённость магнитного поля участка,
Rм = 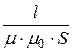 [1/Гн] – магнитное сопротивление участка, соответствую-щее статическому сопротивлению нелинейного резистора в электрической цепи,
[1/Гн] – магнитное сопротивление участка, соответствую-щее статическому сопротивлению нелинейного резистора в электрической цепи,
m0 = 4p×10 -7 Гн/м – магнитная постоянная,
m – относительная магнитная проницаемость материала участка, нелинейно зависящая от магнитной индукции.
При постоянных потоках зависимость между В и H задаётся кривой намагничивания (рис. 2.22,б) материала сердечника, хотя часто выражается формулой В = mm0×H.
Для воздушных зазоров m = 1 и ВВ = m0×H.
Обычно расчёт вебер-амперной характеристики ведут в следующей последовательности:
1) задают произвольное значение В,
2) рассчитывают соответствующее значение потока Ф = В×S,
3) определяется по кривой намагничивания соответствующее принятому В значение H (рис. 2.22,б),
4) находят Uм = H×l.
Примечание: при наличии воздушного зазора на участке пользуются следующей приближённой формулой:
НВ = 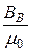 = 0,8×106×ВВ,
= 0,8×106×ВВ,
где HВ[А/м], ВВ[Тл=Вб/м2].
Тогда UмАВ = H×l + HВ×lВ.
Расчёты повторяют для диапазона изменений индукции от нуля до 1,5¸1,7 Тл, сводят их в таблицы и строят вебер-амперные характеристики (рис. 2.22,в), где 1– ВбАХ при отсутствии воздушного зазора на участке,
2– ВбАХ при наличии воздушного зазора.
В дальнейшем методика расчёта магнитных цепей совпадает с методикой расчёта нелинейных электрических цепей и для наглядности расчётов можно составлять эквивалентную расчётную схему – аналог электрической цепи.
ЗАДАЧА 2.18. На рис. 2.23,а представлен дроссель, являющийся катушкой с числом витков W = 500, намотанной на сердечник из электротехнической стали 1512, кривая намагничивания которой приведена в табл. 2.19. Длина средней линии магнитопровода l = 100 см, сечение стали S = 16 см2. Воздушный зазор отсутствует lВ = 0. Рассчитать и построить вебер-амперную характеристику катушки.
Таблица 2.19
Дата добавления: 2016-01-18; просмотров: 2669;
