Взаимодействие токов. Магнитная индукция
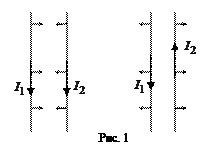 Электрические токи взаимодействуют между собой. Как показывает опыт, два прямолинейных параллельных проводника, по которым текут токи, притягиваются, если токи в них имеют одинаковое направление, и отталкиваются, если токи противоположны по направлению (рис. 1). При этом сила их взаимодействия на единицу длины проводника прямо пропорциональна силе тока в каждом из проводников и обратно пропорциональна расстоянию между ними. Закон взаимодействия токов был установлен Андре Мари Ампером в 1820 г. экспериментально.
Электрические токи взаимодействуют между собой. Как показывает опыт, два прямолинейных параллельных проводника, по которым текут токи, притягиваются, если токи в них имеют одинаковое направление, и отталкиваются, если токи противоположны по направлению (рис. 1). При этом сила их взаимодействия на единицу длины проводника прямо пропорциональна силе тока в каждом из проводников и обратно пропорциональна расстоянию между ними. Закон взаимодействия токов был установлен Андре Мари Ампером в 1820 г. экспериментально.
В металлах суммарный заряд положительно заряженной ионной решетки и отрицательно заряженных свободных электронов равен нулю. Заряды распределены в проводнике равномерно. Таким образом, электрическое поле вокруг проводника отсутствует. Именно поэтому проводники при отсутствии тока не взаимодействуют друг с другом.
Однако при наличии тока (упорядоченного движения свободных носителей заряда) между проводниками возникает взаимодействие, которое принято называть магнитным.
В современной физике магнитное взаимодействие токов трактуется как релятивистский эффект, возникающий в системе отсчета, относительно которой имеет место упорядоченное движение зарядов [2]. В данном пособии будем использовать понятие магнитного поля как свойство пространства, окружающего электрический ток. Существование магнитного поля тока проявляется при взаимодействии с другими проводниками с током (закон Ампера), или при взаимодействии с движущейся заряженной частицей (сила Лоренца, подразд. 2.1), или при отклонении магнитной стрелки, помещенной вблизи проводника с током (опыт Эрстеда).
Для характеристики магнитного поля тока введем понятие вектора магнитной индукции. Для этого, аналогично тому как при определении характеристик электростатического поля использовалось понятие пробного точечного заряда [3], при введении вектора магнитной индукции будем использовать пробный контур с током. Пусть это будет плоский замкнутый 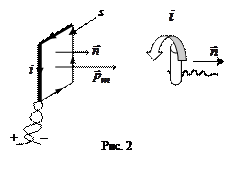 контур произвольной формы и малых размеров. Настолько малых, что в точках места его расположения магнитное поле можно считать одинаковым. Ориентацию контура в пространстве будем характеризовать вектором нормали к контуру, связанным с направлением тока в нем правилом правого винта (буравчика): при вращении ручки буравчика в направлении тока
контур произвольной формы и малых размеров. Настолько малых, что в точках места его расположения магнитное поле можно считать одинаковым. Ориентацию контура в пространстве будем характеризовать вектором нормали к контуру, связанным с направлением тока в нем правилом правого винта (буравчика): при вращении ручки буравчика в направлении тока 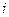 (рис. 2) поступательное движение кончика буравчика определяет направление единичного вектора нормали
(рис. 2) поступательное движение кончика буравчика определяет направление единичного вектора нормали 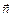 к плоскости контура.
к плоскости контура.
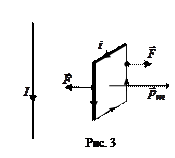 Характеристикой пробного контура является его магнитный момент
Характеристикой пробного контура является его магнитный момент 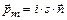 , где s – площадь пробного контура.
, где s – площадь пробного контура.
 Если поместить пробный контур с током в выбранную точку рядом с прямым током, то токи будут взаимодействовать. При этом на пробный контур с током будет действовать вращательный момент пары сил М (рис. 3). Величина этого момента, как показывает опыт, зависит от свойств поля в данной точке (контур мал по размеру) и от свойств контура (его магнитного момента).
Если поместить пробный контур с током в выбранную точку рядом с прямым током, то токи будут взаимодействовать. При этом на пробный контур с током будет действовать вращательный момент пары сил М (рис. 3). Величина этого момента, как показывает опыт, зависит от свойств поля в данной точке (контур мал по размеру) и от свойств контура (его магнитного момента).
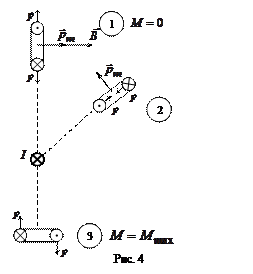
На рис. 4, представляющем собой сечение рис. 3 горизонтальной плоскостью, показаны несколько положений пробного контура с током в магнитном поле прямого тока I. Точка в кружке обозначает направление тока к наблюдателю. Крест обозначает направление тока за рисунок. Положение 1 соответствует устойчивому равновесию контура (М = 0), когда силы растягивают его. Положение 2 соответствует неустойчивому равновесию (М = 0). В положении 3 на пробный контур с током действует максимальный вращающий момент сил. В зависимости от ориентации контура величина вращающего момента может принимать любые значения от нуля до максимального 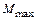 . Как показывает опыт, в любой точке
. Как показывает опыт, в любой точке 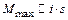 , т. е. максимальное значение механического момента пары сил зависит от величины магнитного момента пробного контура и не может служить характеристикой магнитного поля в исследуемой точке. Отношение максимального механического момента пары сил к магнитному моменту пробного контура не зависит от последнего и может служить характеристикой магнитного поля. Эта характеристика называется магнитной индукцией (индукцией магнитного поля)
, т. е. максимальное значение механического момента пары сил зависит от величины магнитного момента пробного контура и не может служить характеристикой магнитного поля в исследуемой точке. Отношение максимального механического момента пары сил к магнитному моменту пробного контура не зависит от последнего и может служить характеристикой магнитного поля. Эта характеристика называется магнитной индукцией (индукцией магнитного поля)
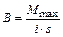 .
.
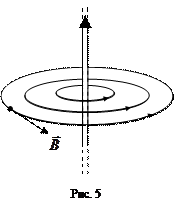 Введем ее как векторную величину. За направление вектора магнитной индукции
Введем ее как векторную величину. За направление вектора магнитной индукции 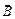 будем принимать направление магнитного момента пробного контура с током, помещенного в исследуемую точку поля, в положении устойчивого равновесия (положение 1 на рис. 4). Это направление совпадает с направлением северного конца магнитной стрелки, помещенной в эту точку. Из сказанного следует, что
будем принимать направление магнитного момента пробного контура с током, помещенного в исследуемую точку поля, в положении устойчивого равновесия (положение 1 на рис. 4). Это направление совпадает с направлением северного конца магнитной стрелки, помещенной в эту точку. Из сказанного следует, что 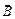 характеризует силовое действие магнитного поля на ток и, следовательно, является аналогом напряженности поля в электростатике. Поле вектора
характеризует силовое действие магнитного поля на ток и, следовательно, является аналогом напряженности поля в электростатике. Поле вектора 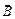 можно представить при помощи линий магнитной индукции. В каждой точке линии вектор
можно представить при помощи линий магнитной индукции. В каждой точке линии вектор 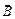 направлен по касательной к ней. Так как вектор магнитной индукции в любой точке поля имеет определенное направление, то и направление линии магнитной индукции – единственное в каждой точке поля. Следовательно, линии магнитной индукции, так же как и силовые линии электрического поля, не пересекаются. На рис. 5 представлено несколько линий индукции магнитного поля прямого тока, изображенных в плоскости, перпендикулярной току. Они имеют вид замкнутых окружностей с центрами на оси тока.
направлен по касательной к ней. Так как вектор магнитной индукции в любой точке поля имеет определенное направление, то и направление линии магнитной индукции – единственное в каждой точке поля. Следовательно, линии магнитной индукции, так же как и силовые линии электрического поля, не пересекаются. На рис. 5 представлено несколько линий индукции магнитного поля прямого тока, изображенных в плоскости, перпендикулярной току. Они имеют вид замкнутых окружностей с центрами на оси тока.
Следует отметить, что линии индукции магнитного поля всегда замкнуты. Это отличительная черта вихревого поля, в котором поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю (теорема Гаусса в магнетизме).
1.2. Закон Био–Савара–Лапласа.
Принцип суперпозиции в магнетизме
Био и Савар провели в 1820 г. исследование магнитных полей токов различной формы. Они установили, что магнитная индукция во всех случаях пропорциональна силе тока, создающего магнитное поле. Лаплас проанализировал экспериментальные данные, полученные Био и Саваром, и нашел, что магнитное поле тока I любой конфигурации может быть вычислено как векторная сумма (суперпозиция) полей, создаваемых отдельными элементарными участками тока.
 Длина
Длина 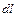 каждого участка тока настолько мала, что его можно считать прямым отрезком, расстояние от которого до точки наблюдения много больше
каждого участка тока настолько мала, что его можно считать прямым отрезком, расстояние от которого до точки наблюдения много больше 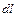 . Удобно ввести понятие элемента тока
. Удобно ввести понятие элемента тока 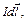 где направление вектора
где направление вектора 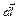 совпадает с направлением тока I, а его модуль равен
совпадает с направлением тока I, а его модуль равен 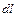 (рис. 6).
(рис. 6).
Для индукции магнитного поля 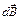 , создаваемого элементом тока
, создаваемого элементом тока 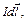 в точке, находящейся на расстоянии r от него (рис. 6), Лаплас вывел формулу, справедливую для вакуума:
в точке, находящейся на расстоянии r от него (рис. 6), Лаплас вывел формулу, справедливую для вакуума:
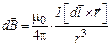 . (1.1)
. (1.1)
Формула закона Био–Савара–Лапласа (1.1) написана в системе СИ, в которой постоянная 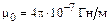 называется магнитной постоянной.
называется магнитной постоянной.
Уже отмечалось, что в магнетизме, как и в электричестве, имеет место принцип суперпозиции полей, т. е. индукция магнитного поля, создаваемого системой токов, в данной точке пространства равна векторной сумме индукций магнитных полей, создаваемых в этой точке каждым из токов в отдельности:
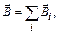
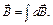 (1.2)
(1.2)
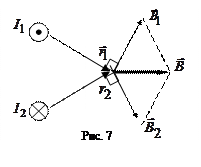 На рис. 7 приведен пример построения вектора магнитной индукции
На рис. 7 приведен пример построения вектора магнитной индукции 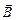 в поле двух параллельных и противоположных по направлению токов
в поле двух параллельных и противоположных по направлению токов 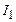 и
и 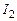 :
: 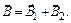

1.3. Применение закона Био–Савара–Лапласа.
Магнитное поле прямого тока
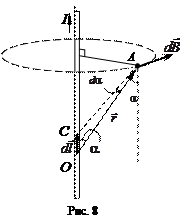
Рассмотрим отрезок прямого тока. Элемент тока 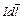 создает магнитное поле, индукция которого в точке А (рис. 8) по закону Био–Савара–Лапласа находится по формуле:
создает магнитное поле, индукция которого в точке А (рис. 8) по закону Био–Савара–Лапласа находится по формуле:
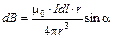 , (1.3)
, (1.3)
где 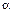 – угол между направлением тока и вектором
– угол между направлением тока и вектором 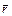 , характеризующим положение точки А относительно
, характеризующим положение точки А относительно 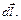
На рис. 9 представлен фрагмент рис. 8. Опустив перпендикуляр из точки С на сторону ОА, получим два прямоугольных треугольника. Из треугольника ODC следует, что СD = 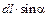 , а из треугольника CDA следует, что CD=
, а из треугольника CDA следует, что CD= 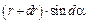 .
.
Учитывая, что 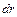 и
и 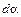 бесконечно малые величины, получим
бесконечно малые величины, получим
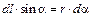 . (1.4)
. (1.4)
После подстановки (1.4) в (1.3) получим:
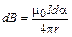 .
.
Из рис. 8 следует, что 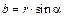 , где b – расстояние от прямого тока до рассматриваемой точки А. Следовательно,
, где b – расстояние от прямого тока до рассматриваемой точки А. Следовательно,
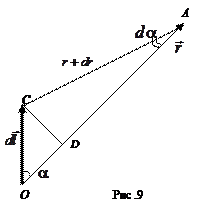
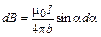 .
.
По принципу суперпозиции 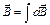 . В точке А все
. В точке А все 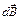 от различных элементов отрезка прямого тока имеют одинаковое направление. Величина магнитной индукции в точке А равна алгебраической сумме
от различных элементов отрезка прямого тока имеют одинаковое направление. Величина магнитной индукции в точке А равна алгебраической сумме 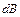 от всех элементов прямого тока:
от всех элементов прямого тока:
|
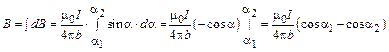 .
.
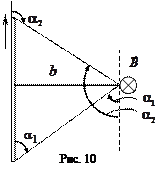 Таким образом, для индукции магнитного поля отрезка прямого тока конечной длины (рис. 10) получаем формулу
Таким образом, для индукции магнитного поля отрезка прямого тока конечной длины (рис. 10) получаем формулу
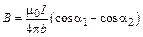 . (1.5)
. (1.5)
В случае бесконечно длинного прямого проводника с током 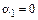 ,
, 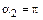 . Следовательно,
. Следовательно, 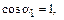
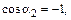
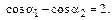 Отсюда следует, что индукция магнитного поля бесконечно длинного прямого проводника с током находится по формуле
Отсюда следует, что индукция магнитного поля бесконечно длинного прямого проводника с током находится по формуле
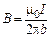 . (1.6)
. (1.6)
1.4. Применение закона Био–Савара–Лапласа.
Магнитное поле кругового тока
Рассмотрим проводник в форме окружности радиуса R, по которому протекает ток I (рис. 11). Разобьем круговой ток на элементы тока 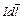 , каждый из которых создает в центре кругового тока (точка О) магнитное поле
, каждый из которых создает в центре кругового тока (точка О) магнитное поле 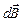 . По закону Био–Савара–Лапласа (1.1), с учетом, что
. По закону Био–Савара–Лапласа (1.1), с учетом, что 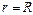 , магнитная индукция, создаваемая элементом тока в точке О, определяется формулой
, магнитная индукция, создаваемая элементом тока в точке О, определяется формулой
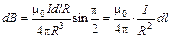 .
.
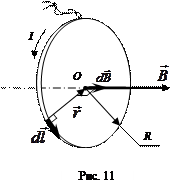 По принципу суперпозиции
По принципу суперпозиции 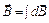 . В точке О все
. В точке О все 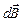 от разных элементов кругового тока имеют одинаковое направление. Следовательно,
от разных элементов кругового тока имеют одинаковое направление. Следовательно,
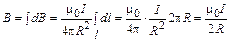 .
.
Таким образом, для индукции магнитного поля в центре кругового тока получаем
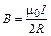 . (1.7)
. (1.7)
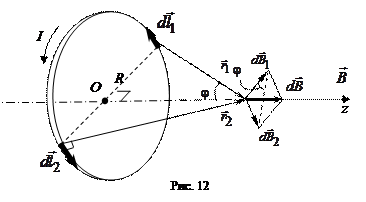
Рассмотрим магнитное поле, создаваемое круговым током в других точках на оси z (рис. 12).
|
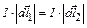 ), расположенная симметрично относительно оси z, создает в точках на оси магнитное поле:
), расположенная симметрично относительно оси z, создает в точках на оси магнитное поле: 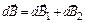 (
( 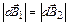 ). Вектор
). Вектор 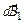 в соответствии с законом Био–Савара–Лапласа направлен перпендикулярно плоскости, содержащей вектора
в соответствии с законом Био–Савара–Лапласа направлен перпендикулярно плоскости, содержащей вектора 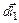 и
и 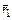 . Вектор
. Вектор 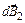 направлен перпендикулярно плоскости, содержащей вектора
направлен перпендикулярно плоскости, содержащей вектора 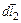 и
и 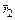 . Вектора
. Вектора 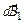 и
и 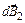 образуют ромб, диагональ которого представляет вектор
образуют ромб, диагональ которого представляет вектор 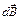 , направленный вдоль оси Оz.
, направленный вдоль оси Оz.
Как следует из рис. 12,
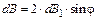 .
.
Учитывая, что 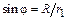 , по закону Био–Савара–Лапласа
, по закону Био–Савара–Лапласа
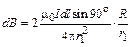 .
.
Так как 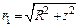 ,
, 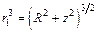 , получаем
, получаем
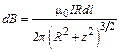 .
.
По принципу суперпозиции результирующий вектор 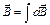 также направлен вдоль оси z, поэтому
также направлен вдоль оси z, поэтому
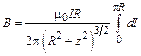 .
.
Окончательное выражение для индукции в точках на оси кругового тока имеет вид
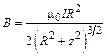 .
.
1.5. Магнитное поле,
создаваемое движущейся заряженной частицей
Как было отмечено в подразд. 1.2, элемент тока 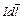 создает магнитное поле. Но такой элемент тока представляет собой совокупность упорядоченно движущихся заряженных частиц. Логично предположить, что в основе появления магнитного поля лежит движение отдельно взятой заряженной частицы, а упорядоченное движение множества таких частиц (носителей тока) приводит к пропорциональному увеличению значения магнитной индукции. Такое предположение подтверждается тем, что пучки движущихся заряженных частиц, например электронов в электронно-лучевой трубке, создают магнитное поле [4].
создает магнитное поле. Но такой элемент тока представляет собой совокупность упорядоченно движущихся заряженных частиц. Логично предположить, что в основе появления магнитного поля лежит движение отдельно взятой заряженной частицы, а упорядоченное движение множества таких частиц (носителей тока) приводит к пропорциональному увеличению значения магнитной индукции. Такое предположение подтверждается тем, что пучки движущихся заряженных частиц, например электронов в электронно-лучевой трубке, создают магнитное поле [4].
Вычислим значение индукции магнитного поля 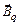 , создаваемого отдельной движущейся заряженной частицей, исходя из закона Био–Савара–Лапласа:
, создаваемого отдельной движущейся заряженной частицей, исходя из закона Био–Савара–Лапласа:
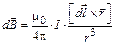 .
.
Для простоты предположим, что все носители тока в элементе тока 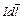 имеют одинаковый заряд
имеют одинаковый заряд 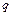 и одинаковую скорость упорядоченного движения
и одинаковую скорость упорядоченного движения 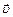 . Пусть концентрация заряженных частиц, т. е. их число в единице объема, равна n, а площадь поперечного сечения элемента тока равна S. Тогда, в предположении равномерного распределения тока по сечению проводника, сила тока
. Пусть концентрация заряженных частиц, т. е. их число в единице объема, равна n, а площадь поперечного сечения элемента тока равна S. Тогда, в предположении равномерного распределения тока по сечению проводника, сила тока 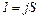 . Плотность тока
. Плотность тока 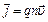 [5]. Выражение для элемента тока можно преобразовать следующим образом:
[5]. Выражение для элемента тока можно преобразовать следующим образом:
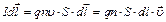 ,
,
где учтено, что векторы 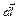 и
и 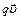 имеют одинаковое направление. Так как
имеют одинаковое направление. Так как 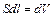 – объем элемента тока, то
– объем элемента тока, то 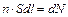 – число носителей тока в этом элементе. Тогда
– число носителей тока в этом элементе. Тогда 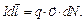 Умножим обе части равенства векторно на
Умножим обе части равенства векторно на 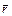 :
: 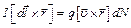 – и подставим в (1.1). В результате получим
– и подставим в (1.1). В результате получим
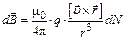 .
.
Последнее равенство перепишем в виде
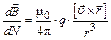 ,
,
где 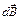 – индукция магнитного поля, создаваемого совокупностью движущихся заряженных частиц (
– индукция магнитного поля, создаваемого совокупностью движущихся заряженных частиц ( 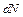 – число частиц). Отсюда индукция магнитного поля
– число частиц). Отсюда индукция магнитного поля 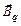 в точке А от одной заряженной частицы, находящейся на расстоянии r от точки А (рис. 13), будет равна
в точке А от одной заряженной частицы, находящейся на расстоянии r от точки А (рис. 13), будет равна
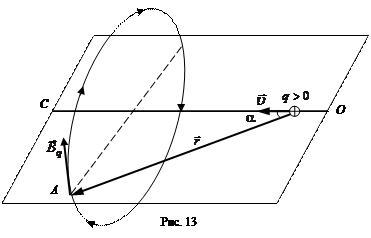
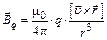 . (1.8)
. (1.8)
Модуль магнитной индукции
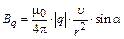 . (1.9)
. (1.9)
Из (1.8) и (1.9) следует: неподвижная 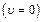 заряженная частица не создает магнитного поля (
заряженная частица не создает магнитного поля ( 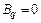 ); индукция магнитного поля обратно пропорциональна квадрату расстояния от заряженной частицы до рассматриваемой точки; индукция магнитного поля равна нулю на прямой, совпадающей с направлением скорости частицы
); индукция магнитного поля обратно пропорциональна квадрату расстояния от заряженной частицы до рассматриваемой точки; индукция магнитного поля равна нулю на прямой, совпадающей с направлением скорости частицы 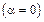 ; максимальное значение магнитной индукции имеет место в направлениях, ортогональных вектору ее скорости
; максимальное значение магнитной индукции имеет место в направлениях, ортогональных вектору ее скорости 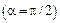 .
.
Из выражения (1.8) следует, что вектор 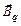 ортогонален плоскости, в которой находятся вектора
ортогонален плоскости, в которой находятся вектора 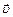 и
и 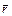 (рис. 13). Для частицы с положительным зарядом q направление вектора
(рис. 13). Для частицы с положительным зарядом q направление вектора 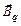 удобно определять по правилу правого винта: при ввинчивании буравчика в направлении скорости
удобно определять по правилу правого винта: при ввинчивании буравчика в направлении скорости 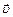 конец ручки буравчика вращается в направлении линий магнитной индукции. При этом линии магнитной индукции представляют собой окружности, центры которых находятся на прямой ОС (рис. 13). Плоскости, в которых лежат линии магнитной индукции, перпендикулярны ОС. Одна из линий магнитной индукции показана на рис. 13. Если
конец ручки буравчика вращается в направлении линий магнитной индукции. При этом линии магнитной индукции представляют собой окружности, центры которых находятся на прямой ОС (рис. 13). Плоскости, в которых лежат линии магнитной индукции, перпендикулярны ОС. Одна из линий магнитной индукции показана на рис. 13. Если 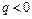 , то линии индукции имеют направление, противоположное указанному.
, то линии индукции имеют направление, противоположное указанному.
| |
| |
При применении формулы (1.8) предполагается, что всякое изменение положения частицы в пространстве, а также величины и направления ее скорости 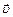 , мгновенно скажется на величине и направлении индукции
, мгновенно скажется на величине и направлении индукции 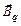 . В действительности это не так. Если частица изменила свое положение или скорость, то только через время
. В действительности это не так. Если частица изменила свое положение или скорость, то только через время 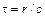 (τ – время запаздывания,
(τ – время запаздывания, 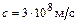 – скорость света) сигнал об этом дойдет до точки наблюдения. По этой причине (1.9) можно применять, если
– скорость света) сигнал об этом дойдет до точки наблюдения. По этой причине (1.9) можно применять, если 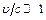 .
.
1.6. Теорема о циркуляции вектора магнитной индукции
(закон полного тока)
Теорема о циркуляции вектора магнитной индукции в вакууме: циркуляция вектора магнитной индукции 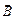 по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на
по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на 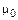 . Иначе говоря,
. Иначе говоря,
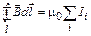 ,
,
 где
где 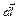 – элементарное перемещение вдоль замкнутого контура l.
– элементарное перемещение вдоль замкнутого контура l.
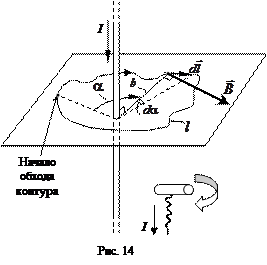
Докажем теорему для случая, когда ток I течет по прямому бесконечно длинному проводнику, а замкнутый контур l расположен в плоскости, перпендикулярной току (рис. 14).
Циркуляция вектора магнитной индукции 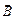 может быть записана в виде
может быть записана в виде
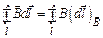 ,
,
где 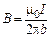 – индукция магнитного поля прямого тока;
– индукция магнитного поля прямого тока; 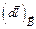 – проекция вектора элементарного перемещения
– проекция вектора элементарного перемещения 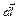 на направление вектора
на направление вектора 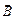 .
.
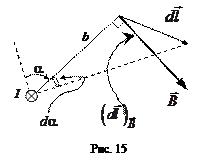 Из рис. 15 видно, что
Из рис. 15 видно, что 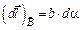 с хорошей степенью точности. Таким образом,
с хорошей степенью точности. Таким образом,
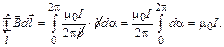 (1.10)
(1.10)
Если изменить направление тока на рис. 14 на противоположное, то изменится направление вектора 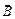 на противоположное в каждой точке пространства. Противоположной по знаку станет циркуляция вектора
на противоположное в каждой точке пространства. Противоположной по знаку станет циркуляция вектора 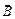 для выбранного направления обхода контура. При этом в равенстве (1.10) ток следует считать отрицательным и подставлять его значение в формулу (1.10) со знаком минус. Таким образом, ток следует считать положительным, если направление обхода контура связано с направлением тока правилом правого винта. В противном случае ток надо считать отрицательным.
для выбранного направления обхода контура. При этом в равенстве (1.10) ток следует считать отрицательным и подставлять его значение в формулу (1.10) со знаком минус. Таким образом, ток следует считать положительным, если направление обхода контура связано с направлением тока правилом правого винта. В противном случае ток надо считать отрицательным.
 Если контур l не охватывает ток (рис. 16), то
Если контур l не охватывает ток (рис. 16), то
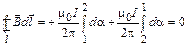 .
.
В случае контура произвольной формы (рис. 17) элементарное перемещение 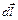 разложим на две составляющие, перпендикулярную
разложим на две составляющие, перпендикулярную 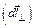 и параллельную
и параллельную 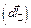 вектору магнитной индукции:
вектору магнитной индукции:
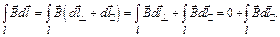
Так как 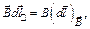 доказательство теоремы для случая контура произвольной формы сводится к рассмотренному выше случаю.
доказательство теоремы для случая контура произвольной формы сводится к рассмотренному выше случаю.
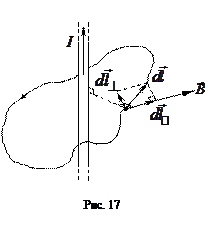 Можно показать, что теорема о циркуляции
Можно показать, что теорема о циркуляции 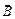 (или закон полного тока) справедлива в общем случае для системы токов произвольной формы и произвольного замкнутого контура:
(или закон полного тока) справедлива в общем случае для системы токов произвольной формы и произвольного замкнутого контура:
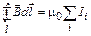 , (1.11)
, (1.11)
где 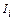 – токи, охватываемые контуром, причем
– токи, охватываемые контуром, причем 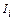 берется с плюсом, если направление
берется с плюсом, если направление 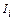 и направление обхода контура связаны правилом правого винта, и с минусом в противном случае.
и направление обхода контура связаны правилом правого винта, и с минусом в противном случае.
Если контур находится в проводящей среде, в которой существует упорядоченное движение зарядов, теорему (1.11) удобно представить в виде
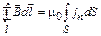 ,
,
где S – любая поверхность, ограниченная контуром l; 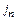 – проекция плотности тока на нормаль к элементу поверхности
– проекция плотности тока на нормаль к элементу поверхности 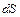 .
.
Дата добавления: 2016-01-20; просмотров: 3485;
