Применение теоремы о циркуляции вектора магнитной индукции. Магнитное поле внутри прямого проводника с током

В качестве примера применения теоремы о циркуляции вектора магнитной индукции для расчета индукции магнитного поля рассмотрим магнитное поле постоянного тока, текущего в бесконечно длинном прямом проводнике цилиндрической формы радиуса R. Замкнутый контур выберем в виде окружности радиуса r, лежащей в плоскости, перпендикулярной оси проводника, и с центром на этой оси (рис. 18).

Пусть направление обхода контура связано с направлением тока правилом правого винта. Из осевой симметрии следует, что во всех точках, равноудаленных от оси проводника с током, индукция магнитного поля одинакова. Проекция вектора магнитной индукции на направление элементарного перемещения совпадает по величине с магнитной индукцией во всех точках замкнутого контура.

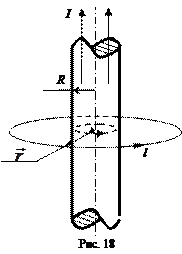Таким образом, для циркуляции вектора магнитной индукции получаем

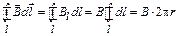, (1.12)

где 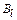– проекция вектора магнитной индукции на направление элементарного перемещения .

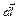Если 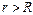, то по закону полного тока:

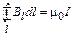. (1.13)

Из сравнения (1.12) и (1.13) следует

,

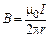что совпадает с ранее полученной формулой (1.6).

Если 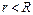, в предположении равномерного распределения тока по сечению проводника, по закону полного тока

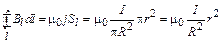, (1.14)

где 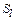– площадь, охватываемая контуром l; j – плотность тока. Из сравнения (1.12) и (1.14) следует

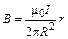. (1.15)

На графике (рис. 19) показана зависимость индукции магнитного поля от расстояния до оси прямого проводника с током.

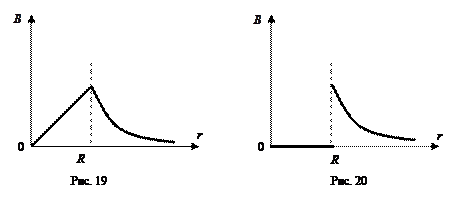
Рассмотрим полый проводник цилиндрической формы в виде трубы, вдоль стенки которой течет постоянный ток. Пусть R – радиус трубы. Замкнутый контур выберем также в форме окружности радиуса r с центром на оси проводника. Пусть 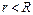. В этом случае контур не охватывает ток и

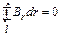. (1.16)

Из сравнения (1.12) и (1.16) следует, что магнитное поле внутри полого проводника с током отсутствует. На рис. 20 представлена зависимость величины индукции магнитного поля в некоторой точке от ее расстояния до оси прямого полого проводника с током.