Магнитное поле тороида

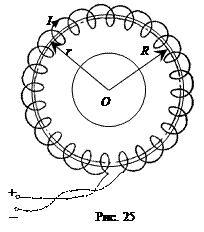
Тороид – устройство, выполненное в виде провода, намотанного плотно виток к витку на каркас, имеющий форму тора (рис. 25). Окружность радиуса R, проходящая через центры витков, называется осью тороида. Пусть I – сила тока, текущего по виткам тороида. Из симметрии рассматриваемого поля следует, что линии магнитной индукции представляют собой окружности с центрами на оси, проходящей через точку О перпендикулярно плоскости рис. 25. Возьмем одну из таких окружностей радиуса r в качестве замкнутого контура и применим теорему о циркуляции . Так как в каждой точке рассматриваемой окружности величина B должна быть одинакова,

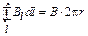. (1.21)

Если контур проходит внутри тороида, то он охватывает ток 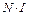, где N – число витков тороида. По теореме о циркуляции

,

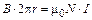откуда получаем

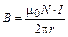. (1.22)

Контур, проходящий вне тороида, не охватывает ток, поэтому для него 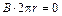. Следовательно, вне тороида магнитная индукция равна нулю.

Для тороида, радиус витка которого много меньше расстояния r от внутренних точек тороида до точки О оси (рис. 25), можно ввести понятие плотности намотки тороида n:

.

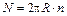Тогда (1.22) примет вид

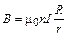. (1.23)

Так как в этом случае 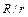мало отличается от единицы, то из (1.23) получается формула, совпадающая с формулой (1.20) для бесконечно длинного соленоида, т. е. величину B можно считать одинаковой во всех точках внутри тороида.