Линейные соотношения в линейных электрических цепях
При изменении в линейной электрической цепи ЭДС (тока) одного из источников или сопротивления в какой-то ветви токи в любой паре ветвей m и n будут связаны между собой соотношением
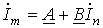 , ,
| (8) |
где А и В – некоторые в общем случае комплексные константы.
Действительно, в соответствии с (1) при изменении ЭДС 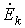 в k – й ветви для тока в m – й ветви можно записать
в k – й ветви для тока в m – й ветви можно записать
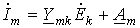
| (9) |
и для тока в n – й ветви –
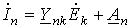 . .
| (10) |
Здесь 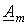 и
и 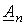 - составляющие токов соответственно в m – й и n – й ветвях, обусловленные всеми остальными источниками, кроме
- составляющие токов соответственно в m – й и n – й ветвях, обусловленные всеми остальными источниками, кроме 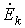 .
.
Умножив левую и правую части (10) на 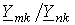 , вычтем полученное соотношением из уравнения (9). В результате получим
, вычтем полученное соотношением из уравнения (9). В результате получим
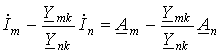 . .
| (11) |
Обозначив в (11) 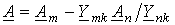 и
и 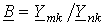 , приходим к соотношению (8).
, приходим к соотношению (8).
Отметим, что в соответствии с законом Ома из уравнения (8) вытекает аналогичное соотношение для напряжений в линейной цепи.
 В качестве примера найдем аналитическую зависимость между токами
В качестве примера найдем аналитическую зависимость между токами 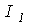 и
и 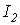 в схеме с переменным резистором на рис. 5, где
в схеме с переменным резистором на рис. 5, где  ;
; 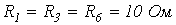 ;
; 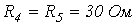 .
.
Коэффициенты А и В можно рассчитать, рассмотрев любые два режима работы цепи, соответствующие двум произвольным значениям 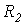 .
.
Выбрав в качестве этих значений 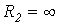 и
и 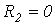 , для первого случая (
, для первого случая ( 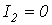 ) запишем
) запишем
 .
.
Таким образом, 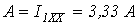 .
.
При 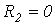 (режим короткого замыкания)
(режим короткого замыкания)
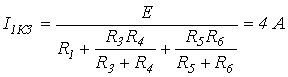 ,
,
откуда
 .
.
На основании (8)
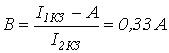 .
.
Таким образом,
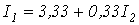 .
.
Дата добавления: 2015-11-28; просмотров: 803;
