Составление матричных соотношений при наличии ветвей с идеальными источниками
В цепи могут иметь место ветви, содержащие только идеальные источники ЭДС или тока. При записи уравнений без использования матричных соотношений такие ветви не вносят каких-либо особенностей в их составление. Однако, если уравнения записываются по второму закону Кирхгофа в матричной форме или используется матричная форма контурных уравнений, то в матрице сопротивлений ветвей Z ветвям, содержащим идеальные источники тока, будут соответствовать диагональные элементы 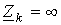 . Поэтому при наличии таких ветвей исходная схема перед составлением уравнений должна быть подвергнута соответствующему преобразованию, иллюстрируемому рис. 3.
. Поэтому при наличии таких ветвей исходная схема перед составлением уравнений должна быть подвергнута соответствующему преобразованию, иллюстрируемому рис. 3.
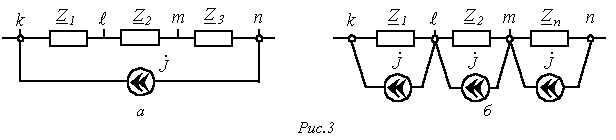
Здесь идеальный источник тока 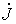 (см. рис. 3,а) включен между узлами k и n. Подключение к узлам l и m по два одинаковых по величине и противоположно направленных источника тока
(см. рис. 3,а) включен между узлами k и n. Подключение к узлам l и m по два одинаковых по величине и противоположно направленных источника тока 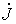 (см. рис. 3,б) не влияет на режим работы цепи, что указывает на эквивалентность замены исходной цепи на рис. 3,а схемой на рис. 3,б.
(см. рис. 3,б) не влияет на режим работы цепи, что указывает на эквивалентность замены исходной цепи на рис. 3,а схемой на рис. 3,б.
Может быть другой случай, когда уравнения в матричной форме записываются по первому закону Кирхгофа или используется матричная форма узловых уравнений, а в цепи имеют место ветви, содержащие только идеальные источники ЭДС. Для таких ветвей соответствующие им диагональные элементы матрицы Y будут равны 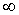 . Поэтому при наличии таких ветвей исходную схему перед составлением уравнений необходимо подвергнуть преобразованию, поясняемому рис. 4.
. Поэтому при наличии таких ветвей исходную схему перед составлением уравнений необходимо подвергнуть преобразованию, поясняемому рис. 4.
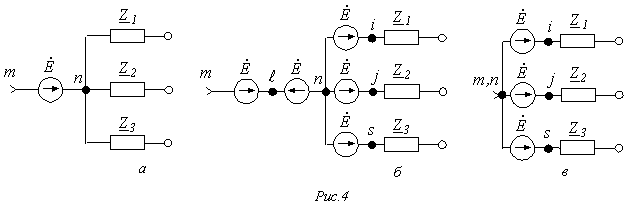
Здесь участок исходной цепи (см. рис. 4,а) содержит ветвь с идеальным источником ЭДС 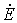 . Включение в каждую ветвь, соединенную с узлом n, источника с ЭДС, равной
. Включение в каждую ветвь, соединенную с узлом n, источника с ЭДС, равной 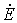 , и направлением действия, указанным на рис. 4,б, позволяет (в силу того, что
, и направлением действия, указанным на рис. 4,б, позволяет (в силу того, что 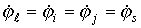 ) трансформировать исходную цепь в схему, представленную на рис. 4,в.
) трансформировать исходную цепь в схему, представленную на рис. 4,в.
|
Литература
- Основытеории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А.Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
- В чем отличие матриц сопротивлений и проводимостей ветвей для цепей с отсутствием и наличием индуктивных связей?
- В чем заключается особенность нумерации ветвей графа при наличии индуктивных связей?
- Какие особенности имеют место при составлении матричных соотношений для цепей, содержащих ветви с идеальными источниками?
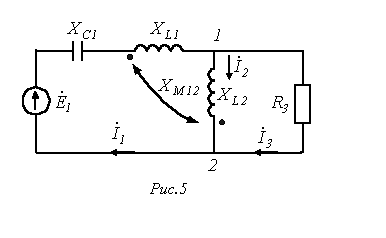
- В цепи на рис. 5
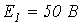 ;
; 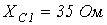 ;
; 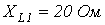 ;
; 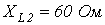 ;
; 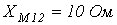 ;
; 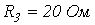 . Приняв, что дерево образовано ветвью 1, составить контурные уравнения в матричной форме и определить токи ветвей.
. Приняв, что дерево образовано ветвью 1, составить контурные уравнения в матричной форме и определить токи ветвей.
| Ответ: |
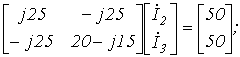
| |
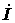
| 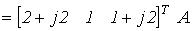 . .
|
- Для цепи на рис.5 составить узловые уравнения в матричной форме, на основании которых затем определить токи ветвей.
Ответ:
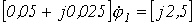 ;
;
.
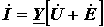
| 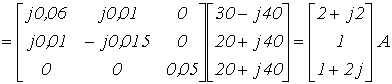
|
Лекция N 12
Дата добавления: 2015-11-28; просмотров: 678;
