Методика проведения корреляционного анализа

Проводится в несколько этапов. На первом этапе необходимо составить выборку фактических данных о значении фактора и соответствующих значений анализируемого показателя. Чем больше исходных данных, тем точнее будут результаты расчетов. Минимальное количество наблюдений – 8, оптимальное – около 30. Результаты наблюдения ранжируются в порядке увеличения показателя-фактора. Затем рассчитываются среднеквадратичные и нормированные отклонения. Обозначим анализируемый показатель У, показатель - фактор Х.

Среднеквадратичные отклонения:

sх = Ö (∑ ( х_i – x_ср))/ n,

sу = Ö (∑ ( y_i – y_ср))/ n,

где n – количество наблюдений;

x_ср , y_ср - среднеарифметические значения соответственно х и у.

Нормированные отклонения:

Тх = ( х_i – x_ср)/ sх;

Ту = ( y_i – y_ср)/ sу.

Коэффициент корреляции:

R = (S Тх * Ту) / n.

По значению коэффициента корреляции определяют тесноту и характер взаимосвязи между показателями. Коэффициент может изменяться в диапазоне от 0 до 1 и может иметь как положительное, так и отрицательное значение. Чем ближе абсолютное значение коэффициента к единице, тем более тесная взаимосвязь между показателями. Положительное значение говорит о прямой взаимосвязи, отрицательное – об обратной. Пороговое значение коэффициента для осуществления дальнейших расчетов – 0,7.

Коэффициент корреляции принимает значения в интервале от -1 до + 1. Принято считать, что если |r|< 0,30, то связь слабая; при |r|= (0,3÷0,7) – средняя; при |r|> 0,70 – сильная, или тесная. Когда |r|= 1 – связь функциональная. Если же r принимает значение около 0, то это дает основание говорить об отсутствии линейной связи между У и X. Однако в этом случае возможно нелинейное взаимодействие. что требует дополнительной проверки и других измерителей, рассматриваемых ниже.

При значении 0,7 индекс детерминации, который равен квадрату коэффициента корреляции, имеет значение 0,49. Индекс детерминации показывает долю влияния выбранного фактора на анализируемый показатель. Очевидно, что если доля влияния выбранного фактора меньше 0,5, дальнейшие расчеты не имеют смысла.

После оценки тесноты взаимосвязи необходимо выбрать функцию, график которой максимально приближенно описывает данную взаимосвязь. Наиболее часто используются графики следующих функций:

У = А + В * Х;

У = А + В * ln X;

У = А + В / Х.

После выбора функции необходимо рассчитать параметры уравнения А и В. Используется метод наименьших квадратов. Решение сводится к решению системы линейных уравнений. Приведен пример системы линейных уравнений для линейной функции:

n * a + b * ∑x = ∑y;

a * ∑x + b * ∑x² = ∑(x*y).

После определения параметров модель можно использовать. Для этого подставляем в формулу желаемое значение фактора и определяем вероятное значение показателя. В качестве проверки можно рассчитать ошибку аппроксимации – процент отклонения значения фактического от значения, рассчитанного по модели:

Ап = ( 1 / n) * ( |У ф – У р| )* 100 / У ф.

Значение ошибки аппроксимации до 10% говорит о наилучшем подборе модели.

Практически для количественной оценки тесноты связи широко используют линейный коэффициент корреляции. Иногда его называют просто коэффициентом корреляции. Если заданы значения переменных Х и У, то он вычисляется по формуле

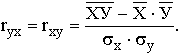
Можно использовать и другие формулы, но результат должен быть одинаковым для всех вариантов расчета.

Коэффициент корреляции принимает значения в интервале от -1 до + 1. Принято считать, что если |r|< 0,30, то связь слабая; при |r|= (0,3÷0,7) – средняя; при |r|> 0,70 – сильная, или тесная. Когда |r|= 1 – связь функциональная. Если же r принимает значение около 0, то это дает основание говорить об отсутствии линейной связи между У и X. Однако в этом случае возможно нелинейное взаимодействие. что требует дополнительной проверки и других измерителей, рассматриваемых ниже.