Стохастические модели

Как уже говорилось выше, стохастические модели – это модели вероятностные. При этом в результате расчетов можно сказать с достаточной степенью вероятности, каково будет значение анализируемого показателя при изменении фактора. Самое частое применение стохастических моделей – прогнозирование.

Стохастическое моделирование является в определенной степени дополнением и углублением детерминированного факторного анализа. В факторном анализе эти модели используются по трем основным причинам:

• необходимо изучить влияние факторов, по которым нельзя построить жестко детерминированную факторную модель (например, уровень финансового левериджа);

• необходимо изучить влияние сложных факторов, которые не поддаются объединению в одной и той же жестко детерминированной модели;
• необходимо изучить влияние сложных факторов, которые не могут быть выражены одним количественным показателем (например, уровень научно-технического прогресса).

В отличие от жестко детерминированного стохастический подход для реализации требует ряда предпосылок:

1. наличие совокупности;
2. достаточный объем наблюдений;
3. случайность и независимость наблюдений;
4. однородность;
5. наличие распределения признаков, близкого к нормальному;
6. наличие специального математического аппарата.

Построение стохастической модели проводится в несколько этапов:

• качественный анализ (постановка цели анализа, определение совокупности, определение результативных и факторных признаков, выбор периода, за который проводится анализ, выбор метода анализа);
• предварительный анализ моделируемой совокупности (проверка однородности совокупности, исключение аномальных наблюдений, уточнение необходимого объема выборки, установление законов распределения изучаемых показателей);
• построение стохастической (регрессионной) модели (уточнение перечня факторов, расчет оценок параметров уравнения регрессии, перебор конкурирующих вариантов моделей);
• оценка адекватности модели (проверка статистической существенности уравнения в целом и его отдельных параметров, проверка соответствия формальных свойств оценок задачам исследования);
• экономическая интерпретация и практическое использование модели (определение пространственно-временной устойчивости построенной зависимости, оценка практических свойств модели).

Основные понятия корреляционного и регрессионного анализа

Корреляционный анализ - совокупность методов математической статистики, позволяющих оценивать коэффициенты, характеризующие корреляцию между случайными величинами, и проверять гипотезы об их значениях на основе расчета их выборочных аналогов.

Корреляционным анализом называется метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными.

Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.

В наиболее общем виде задача статистики (и, соответственно, экономического анализа) в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при интерпретации результатов и др.

Поэтому в данном контексте можно говорить о корреляционном анализе в широком смысле – когда всесторонне характеризуется взаимосвязь. В то же время выделяют корреляционный анализ в узком смысле – когда исследуется сила связи – и регрессионный анализ, в ходе которого оцениваются ее форма и воздействие одних факторов на другие.

Задачи собственнокорреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак.

Задачирегрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.

Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, что дает основание говорить о статистическом изучении взаимосвязей.

Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования.

Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы – параметрические – и принято называть корреляционными.

Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений.

Автокорреляция — статистическая взаимосвязь между случайными величинами из одного ряда, но взятых со сдвигом, например, для случайного процесса — со сдвигом по времени.

Парная корреляция

Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы:

\ Y \ X \	Y1	Y2	...	Yz	Итого	Yi
X1	f11		...	f1z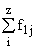
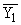
X1	f21		...	f2z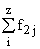
...	...	...	...	...	...	...
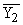
Xr	fk1	k2	...	fkz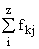
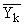
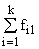
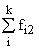
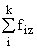
Итого			...		n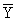
			...			-

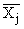
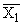
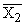
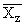
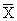
В основу группировки положены два изучаемых во взаимосвязи признака – Х и У. Частоты f_ij показывают количество соответствующих сочетаний Х и У.

Если f_ij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания f_ij допустимо утверждать о связи между Х и У. При этом, если f_ij концентрируется около одной из двух диагоналей, имеет место прямая или обратная линейная связь.

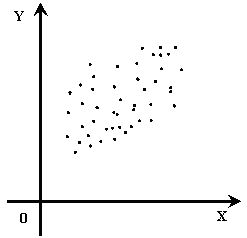
Наглядным изображением корреляционной таблице служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладывают значения Х, по оси ординат – У, а точками показывается сочетание Х и У. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи.

Корреляционным полем называется множество точек {X_i, Y_i} на плоскости XY (рисунки 6.1 - 6.2).

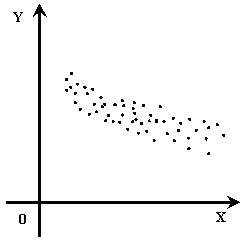
Рисунок 6.1 – Пример корреляционного поля (положительная корреляция)	Рисунок 6.2 – Пример корреляционного поля (отрицательная корреляция)

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет положительный угол наклона ( / ), то имеет место положительная корреляция (пример подобной ситуации можно видеть на рисунке 6.1).

Если точки корреляционного поля образуют эллипс, главная диагональ которого имеет отрицательный угол наклона ( \ ), то имеет место отрицательная корреляция (пример изображен на рисунке 6.2).

Если же в расположении точек нет какой-либо закономерности, то говорят, что в этом случае наблюдается нулевая корреляция.

В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения – одно по X, другое по У. Рассчитаем для каждого Х_i среднее значение У, т.е. , как

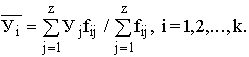
Последовательность точек (X_i, ) дает график, который иллюстрирует зависимость среднего значения результативного признака У от факторного X, – эмпирическую линию регрессии, наглядно показывающую, как изменяется У по мере изменения X.

По существу, и корреляционная таблица, и корреляционное поле, и эмпирическая линия регрессии предварительно уже характеризуют взаимосвязь, когда выбраны факторный и результативный признаки и требуется сформулировать предположения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов.