Соответствия и отношения
ТЕОРИЯ МНОЖЕСТВ
Основные понятия
Множество – понятие неопределяемое, используемое для описания совокупностей математических объектов (чисел, точек, функций и т. д.) Основатель теории множеств немецкий математик Георг Кантор выразил эту мысль следующим образом: «Множество есть многое, понимаемое как единое целое».
В математике множества обозначаются большими буквами латинского алфавита А, В, С, … Х, У, Z. О предметах, составляющих множество, говорят, что они являются элементами множества. Элементы множеств обозначают малыми буквами латинского алфавита: а, b, c, …х, y, z.
Если элемент а принадлежит множеству А, то это записывают: а  А.
А.
Множества могут быть конечными и бесконечными; конечное множество состоит из конечного числа элементов, бесконечное – из бесконечного их числа.
Пример:
Бесконечные множества – числовые множества:
N – множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
I – множество иррациональных чисел,
R – множество действительных чисел.
Множества, не содержащие ни одного элемента, называются пустыми множествами: ?.
Задать множество – значит указать, какие элементы принадлежат множеству, а какие не принадлежат.
Задать множество можно следующими способами:
1) перечислением всех элементов, из которых состоит множество. Например, А = {a,b,c,d,f}.
2) указаниемхарактеристического свойства, т.е. свойства, которым обладают только элементы данного множества и ни один элемент из другого множества не обладает этим свойством. Пример: С – множество натуральных чисел, не превосходящих десяти, С = {x/ х  N, х <10} или
N, х <10} или
С = {1,3,4,5,6,7,8,9}.
 3) перечислением первых элементов множества (перечисление продолжается до тех пор, пока не выявится закономерность получения последующих элементов). Пример: Х = {1,3,5,7,9,…}, У = {2,4,8,16, ...}.
3) перечислением первых элементов множества (перечисление продолжается до тех пор, пока не выявится закономерность получения последующих элементов). Пример: Х = {1,3,5,7,9,…}, У = {2,4,8,16, ...}.
4) в виде промежутков на числовой прямой (используется только для множеств, состоящих из действительных чисел). Примеры:
(2; 5] = {x / x  R , 2 < x
R , 2 < x 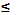 5} (-∞; 3] = {x / x
5} (-∞; 3] = {x / x  R, x
R, x 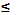 3}
3}
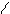
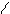
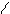
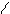
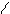
 (2; 5] (-∞; 3]
(2; 5] (-∞; 3]
3. 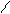
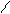
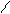
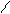
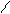
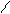
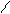
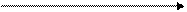 5 R 3 R
5 R 3 R
Рис. 1.1 Рис. 1.2
 Множество В называется подмножеством множества А, если каждый элемент множества В является элементом множества А. В
Множество В называется подмножеством множества А, если каждый элемент множества В является элементом множества А. В 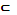 А.
А.
Пример: А = {a,b,c}. Подмножествами множества А будут: собственные подмножества: {a}, {b}, {c}, {a,b}, {b,c}, {a,c}; несобственные подмножества: {a,b,c}, ?.
Два множества А и В называется равными, если они состоят из одних и тех же элементов.
Множество, в которое включаются все рассматриваемые в данный момент множества, называется универсальнымU. На рисунке его принято изображать в виде прямоугольника. Например, при решении задач с действительными числами универсальным будет множество R, а при рассмотрении множества студентов некоторой группы универсальным будет множество студентов университета.

 Наглядно можно изобразить множества с помощью кругов Эйлера (диаграмм Венна).
Наглядно можно изобразить множества с помощью кругов Эйлера (диаграмм Венна).

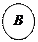

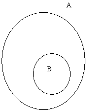
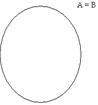
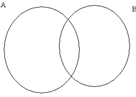
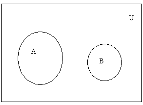
Рис. 1.3 Рис. 1.4 Рис. 1.5 Рис. 1.6
 | |||
 | |||
На рис. 1.3 изображены множества А и В, находящиеся в отношении включения (В 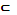 А), на рис. 1.4 – в отношении равенства (А = В), на рис. 1.5 – в отношении пересечения, рис. 1.6 показывает универсальное множество U и его подмножества А и B.
А), на рис. 1.4 – в отношении равенства (А = В), на рис. 1.5 – в отношении пересечения, рис. 1.6 показывает универсальное множество U и его подмножества А и B.
1.2. 

 Операции над множествами
Операции над множествами
Пересечением двух множеств А и В называется множество А∩В, которое состоит из элементов, принадлежащих множествам А и В одновременно.
Символическая запись определения: А∩В = {x/x  A и x
A и x  B}.
B}.
Объединением двух множеств А и В называется множество А 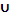 B, которое состоит из элементов, принадлежащих хотя бы одному из множеств А или В.
B, которое состоит из элементов, принадлежащих хотя бы одному из множеств А или В.
Символическая запись определения: А 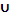 B = {x/x
B = {x/x  A или x
A или x  B}.
B}.
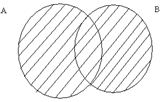
Разностью множеств А и В называется множество А\В, которое состоит из элементов множества А, не принадлежащих множеству В.
Символическая запись определения: А\ В = {x/x  A и x
A и x  B}
B}
Дополнением множества В до множества А называется множество В'А, которое состоит из элементов множества А, не принадлежащих множеству В, при условии, что множество В является подмножеством множества А.
Символическая запись определения: В'А = {x/x  A, x
A, x  B, B
B, B 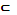 A}
A}
Примеры:
1. Если А = {1,2,3,4,5}, B = {2,4,6,8}, то A∩B = {2,4}, А 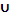 B={1,2,3,4,5,6,8}, А\ В={1,3,5}, В\А ={6,8}.
B={1,2,3,4,5,6,8}, А\ В={1,3,5}, В\А ={6,8}.
2. Если Х – множество любителей психологи, У – множество любителей математики, то А∩В – множество людей, любящих и математику, и психологию; А 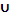 B – множество людей, которые любят хотя бы одну из наук: либо математику, либо психологию (либо обе науки одновременно).
B – множество людей, которые любят хотя бы одну из наук: либо математику, либо психологию (либо обе науки одновременно).
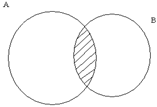
Графическая иллюстрация данных выше определений (рис. 1.7 – 1.11):
 A
A 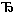 B
B 



 A
A 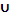 B
B 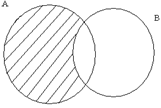

Рис. 1.7  Рис. 1.8 Рис. 1.9
Рис. 1.8 Рис. 1.9

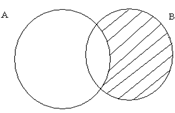
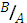
 Рис. 1.10 Рис. 1.11
Рис. 1.10 Рис. 1.11 
Свойства операций объединения и пересечения множеств:
1. Коммутативность А∩В= В∩А, А 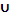 B= B
B= B 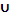 А.
А.
2. Ассоциативность (А∩В)∩С= А∩(В∩С), (А 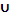 B)
B) 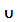 С= А
С= А 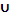 (B
(B 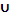 С).
С).
3. Дистрибутивность А∩(В 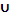 С)=(А∩В)
С)=(А∩В) 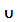 (А∩С), А
(А∩С), А 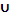 (B∩С)= (А
(B∩С)= (А 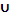 B)∩(А
B)∩(А 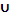 С).
С).
4. Законы де Моргана (А∩В)'= А' 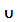 B' , (А
B' , (А 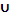 B)'= А'∩В'.
B)'= А'∩В'.
5. А∩А=А, А 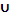 А=А.
А=А.
6. А∩U=А, А∩?= ?.
7. А 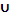 U=U, А
U=U, А 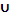 ?=А.
?=А.
Декартовым произведением множеств А и Вназывается множество А?В, состоящее из всех упорядоченных пар вида (х, у), где элемент х взят из множества А, а элемент у взят из множества В.
Символическая запись определения А?В = {(x; у) | X  x , y
x , y  Y}.
Y}.
Если два множества, участвующие в декартовом произведении, равны, то такое декартово произведение называется декартовым квадратом множества.
Пример:
Если Х = {1,2,3}; У = {5, 6}, тогда X?Y = {(1,5), (1,6), (2,5), (2,6), (3,5), (3,6)}, Х?Х = Х2 = {(1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3)}.
Декартовым произведением n множеств А1, А2, … Аn называется множество всевозможных кортежей длины n, в которых первая компонента (координата) принадлежит множеству А1, вторая компонента – множеству А2, и т.д., n-я – множеству An . Кортеж длиныn – это упорядоченная последовательность n элементов, среди которых могут быть одинаковые.Кортеж длины 2 – это упорядоченная пара, кортеж длины 3 – упорядоченная тройка и т. д. Элементы кортежа называются его компонентами или координатами. Два кортежа называются равными, если их длины равны и соответствующие координаты совпадают.
Символическая запись определения декартова произведенияn множеств:
А1? А2 ?… ?An = {(х1, х2, … хn) | х1  A1, х2
A1, х2  A2,… ,хn
A2,… ,хn  An}.
An}.
Способы задания декартова произведения двух множеств:
1. С помощью перечисления упорядоченных пар элементов – пример рассмотрен выше.
2. С помощью графа, на котором два элемента, соединенные стрелкой, обозначают упорядоченную пару:
Х 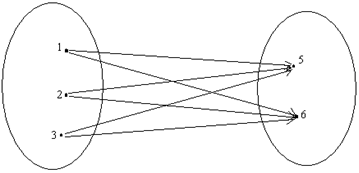 У
У
Рис. 1.12
3. С помощью графика на координатной плоскости:
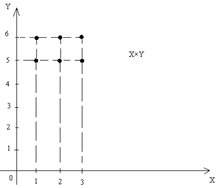
Рис. 1.13
Количество элементов в объединении n(А 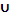 B)и декартовом произведении n(А?В)двух множеств А и В вычисляется соответственно по следующим формулам:
B)и декартовом произведении n(А?В)двух множеств А и В вычисляется соответственно по следующим формулам:
n(А 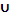 B)=n(A)+n(B)-n (А∩В);
B)=n(A)+n(B)-n (А∩В);
n(А?В)= n(A)·n(B).
В рассмотренном выше примере п(X?Y)=п(Х)·п(У)=3·2=6.
Соответствия и отношения
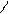 Соответствием R между множествами X и Y называется подмножество R декартова произведения Х?Y : R
Соответствием R между множествами X и Y называется подмножество R декартова произведения Х?Y : R 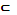 Х?Y.
Х?Y.
Множество Х называют областью отправления данного соответствия, а множество У – его областью прибытия.
Если а  Х, то образом этого элемента называется множество R(а) всех элементов у
Х, то образом этого элемента называется множество R(а) всех элементов у  У, таких, что аRу. Прообразом элемента в
У, таких, что аRу. Прообразом элемента в  У при том же соответствии назовем множество R-1(в) элементов х
У при том же соответствии назовем множество R-1(в) элементов х  Х, таких, что хRв. Образ всего множества Х называется множеством (областью) значений – R(Х), это множество концов всех стрелок. Прообраз всего множества У при соответствии R называют областью определения этого соответствия и обозначают R-1(У), это множество начал всех стрелок.
Х, таких, что хRв. Образ всего множества Х называется множеством (областью) значений – R(Х), это множество концов всех стрелок. Прообраз всего множества У при соответствии R называют областью определения этого соответствия и обозначают R-1(У), это множество начал всех стрелок.
Пример:
Возьмем множество учеников Х={Ваня, Даша, Ира} и множество типов темперамента У={сангвиник, холерик, флегматик, меланхолик}. Построим граф соответствия R: «Ученик х обладает темпераментом у».
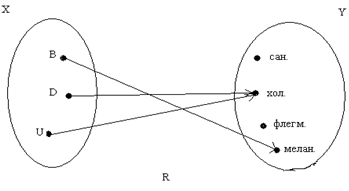
Рис. 1.14
На рис. 1.14: R(Ваня)= {меланхолик}, R(Даша)= {холерик}, R(Ира)={холерик}, R-1 (сангвиник)= ?, R-1(флегматик)= ?, R-1 (холерик)= {Даша, Ира}, R-1(меланхолик) = {Ваня}. Область определения соответствия R-1(У)= =Х={Ваня, Даша, Ира}, множество значений R(Х)= {холерик, меланхолик}.
______________________________________________________________
Если при соответствии R образ каждого элемента х  Х или пуст, или содержит лишь один элемент, то R называют функциональным соответствием или функцией. Другими словами, соответствие R функционально, если из того, что хRу1 и хRу2, можно сделать вывод, что у1=у2.
Х или пуст, или содержит лишь один элемент, то R называют функциональным соответствием или функцией. Другими словами, соответствие R функционально, если из того, что хRу1 и хRу2, можно сделать вывод, что у1=у2.
Соответствие R, для которого области отправления и прибытия совпадают, называется отношением, заданным на множестве Х. Для элементов х и у из множества Х, связанных отношением R, можно записать: хRу или R(х)=у.
Отношение R, заданное на множестве Х, называется рефлексивным, если для всех х  Х выполняется хRх.
Х выполняется хRх.
Отношение R, заданное на множестве Х, называется антирефлексивным, если ни для какого х  Х не выполняется хRх.
Х не выполняется хRх.
Отношение R, заданное на множестве Х, называется симметричным, если для всех х  Х, у
Х, у  Х выполняется: если хRу, то уRх.
Х выполняется: если хRу, то уRх.
Отношение R, заданное на множестве Х, называется асимметричным, если ни для каких х  Х, у
Х, у  Х не выполняется: если хRу, то уRх.
Х не выполняется: если хRу, то уRх.
Отношение R, заданное на множестве Х, называется антисимметричным, если для х  Х, у
Х, у  Х выполняется: если хRу и уRх, то х=у.
Х выполняется: если хRу и уRх, то х=у.
Отношение R, заданное на множестве Х, называется транзитивным, если для х  Х, у
Х, у  Х, z
Х, z  Х, выполняется: если хRу и уRz, то хRz.
Х, выполняется: если хRу и уRz, то хRz.
Пример:
Рассмотрим отношение R: «учиться в одной группе» на множестве студентов. Проверим выполнение следующих свойств:
1. Рефлексивность: для любого студента х выполняется хRх, т.е. «студент х учится в одной группе сам с собой» - и.
2. Симметричность: для двух студентов х и у выполняется если хRу, то уRх, т.е. «если студент х учится в одной группе со студентом у, то студент у учится в одной группе со студентом х» - и.
3. Транзитивность: для трех студентов х, у, z выполняется: если хRу и уRz, то хRz, т.е. «если студент х учится в одной группе со студентом у, а студент у учится в одной группе со студентом z, то студенты х и z учатся в одной группе» - и.
Отношение R на множестве Х называется отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно. Рассмотренное в примере отношение «учиться в одной группе»на множестве студентов является отношением эквивалентности.
Отношение R на множестве Х называется отношением толерантности, если оно рефлексивно и симметрично. Примером отношения толерантности может служить отношение «быть знакомым» на множестве людей.
Отношение R на множестве Х называется отношением строгого порядка, если оно антирефлексивно, асимметрично, транзитивно. Примерами являются отношения «выше», «дальше», «тяжелее».
Отношение R на множестве Х называется отношением нестрогого порядка, если оно рефлексивно, антисимметрично, транзитивно. Примерами являются отношения «не выше», «не меньше», «не больше».
Рассмотренные отношения и их свойства находят применение при составлении тестов, в вопросах голосования и т.д.
Дата добавления: 2016-01-16; просмотров: 1668;
