Фононы и их распределение по энергиям
(распределение Бозе-Эйнштейна)
Атомы, ионы, находящиеся в узлах кристаллической решетки, являются квантовыми гармоническими осцилляторами.
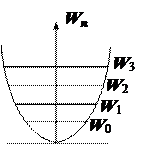 |
Из решения уравнения Шредингера следует, что энергия таких частиц квантуется.
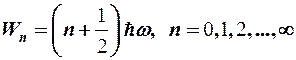
Согласно принципу минимума энергии наиболее выгодное состояние – состояние с энергией W0 – основное (невозбужденное) состояние.
При сообщении твердому телу дополнительной энергии происходит возбуждение осцилляторов – они переходят на более высокие уровни.
Но возбужденные состояния – короткоживущие. Пробыв в них короткое время, осцилляторы переходят на ниже лежащие состояния. При этом правило отбора утверждает, что
Dn = 1,
т. е. переходы происходят на соседний нижележащий уровень.
При этом осциллятор теряет энергию  , которая уносится в виде низкочастотной тепловой волны по кристаллу.
, которая уносится в виде низкочастотной тепловой волны по кристаллу.
Порцию (квант) такой тепловой волны по аналогии с порцией (квантом) электромагнитной волны – фотоном, назвали фононом.
Т. о. фонон – это квазичастица, так как существует только в твердом теле, не имеющая электрического заряда, не существующая в покое, а всегда движущаяся со скоростью звука в твердом теле.
Энергия фонона:
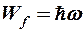 . (12-2)
. (12-2)
При этом для фононов нет запрета Паули, спин у них целочисленный s = 1, значит, они относятся к классу бозонов.
Функция распределения Бозе-Эйнштейна позволяет вычислить среднее число бозонов (фононов) из общего их числа, находящихся в данном квантовом состоянии или вероятность того, что данный фонон обладает энергией 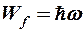 .
.
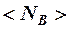 =
= 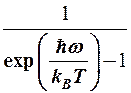 . (12-3)
. (12-3)
Другими словами функция распределения Бозе-Эйнштейна определяет вероятность заселения данного квантового состояния.
 Графически
Графически
При 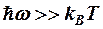 ®
® 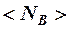 »
» 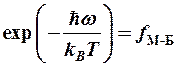 - классическое распределение Максвелла-Больцмана.
- классическое распределение Максвелла-Больцмана.
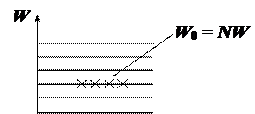 |
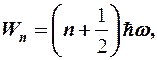
где  - энергия осциллятора.
- энергия осциллятора.
n = 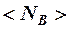 с энергией
с энергией  .
.
Т. к. энергия одного фонона 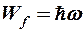 , а их число в данном квантовом состоянии определяется (12-3), тогда средняя энергия одного квантового состояния гармонического осциллятора (средняя энергия всех фононов в данном квантовом состоянии):
, а их число в данном квантовом состоянии определяется (12-3), тогда средняя энергия одного квантового состояния гармонического осциллятора (средняя энергия всех фононов в данном квантовом состоянии):
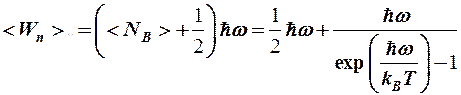 . (*)
. (*)
Дата добавления: 2016-01-11; просмотров: 1560;
