Основы построения сетевой модели

Сетевые методы планирования и управления используются для планирования и управления сложных динамических разработок.

В основе СПУ лежит сетевая модель разработки.

Сетевая модель (сетевой график) – это графическое изображение всех работ, всех операций в их строго технологической последовательности, которые нужно выполнить, чтобы что-то построить или что-то создать.

Преимущество СПУ: они позволяют из всего перечня работ выделить те работы, от своевременности выполнения которых зависит срок сдачи объекта в эксплуатацию (критические работы).

СПУ позволяют установить, какими запасами времени располагают работы, не лежащие на критическом пути. Знания этих резервов используются при корректировке планов.

Основная область применения СПУ - строительство объектов и организация производственных процессов.

Основными элементами СГ являются:

- работа;

- событие;

- путь.

Работа — это процесс или действие, приводящее к определенному результату.

Существует три вида работ:

- действительная — протяженный во времени процесс, требующий
затрат ресурсов и времени;

- работа-ожидание — протяженный во времени процесс, не требующий
затрат;

- фиктивная – логическая связь между двумя или несколькими работами, не требующая затрат ни материальных, ни труда, ни времени;

она указывает на возможность одной работы непосредственно зависеть от результатов другой;

продолжительность фиктивной работы равна нулю.

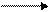На СГ действительная работа и работа-ожидание обозначаются так

Работа i-j (i-j - код работы)

Над каждой работой указывается либо продолжительность ее выполнения (в часах, днях, месяцах), либо номер, либо наименование работы.

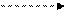Фиктивная работа на СГ обозначается

Работа i-j

Событие определяет окончание одной или нескольких работ и одновременно начало последующих работ.

Любая работа соединяет только два события.

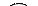
i - номер события, событие i-oe

Событие, из которого выходит работа, называется начальным или предшествующим по отношению к данной работе.

Событие, в которое заходит работа, называется конечным или последующим для данной работы.

I - начальное событие

j - конечное событие

Событие, которое не имеет предшествующих работ, называется исходным событием.

Событие, которое не имеет последующих работ, называется завершающим.

Все остальные события являются промежуточными.

Путь – это непрерывная последовательность работ между двумя событиями.

Полный путь – непрерывная последовательность работ от исходного события до завершающего.

Укороченный путь – непрерывная последовательность работ от исходного события до любого промежуточного, либо от какого-нибудь промежуточного события до завершающего.

Критический путь – наибольший по продолжительности полный путь на сетевом графике, он определяет min необходимое время для выполнения всего комплекса работ (т. е. за меньшее время работы выполнить нельзя).

Подкритический путь – по продолжительности близкий к критическому и при определенных условиях он может стать критическим.

Правила построения сетевых графиков:

1.Необходимо установить, какие работы должны быть завершены до
начала данной.

2.Необходимо определить, какие работы могут выполняться
одновременно.

3.Необходимо определить, какие работы могут начинаться после
завершения данной работы.

4.Построение СГ нужно осуществлять слева направо.

5.На СГ не должно быть так называемых "тупиковых" и "хвостовых"
событий

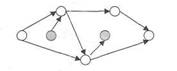
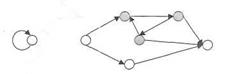
6. На СГ не должно быть изолированных участков, замкнутых контуров и петель.

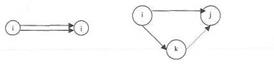
7. Любые два события могут быть связаны не более, чем одной работой. Если на СГ обнаружены параллельные работы, то нужно ввести фиктивное событие и фиктивную работу.

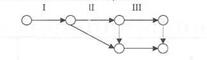
8. Если для начала выполнения некоторых работ необходимо только частичное выполнение предшествующей работы, то она должна быть разбита на части и представлена в виде последовательно выполняемых самостоятельных работ.

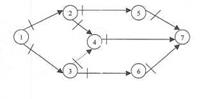
9. На СГпо возможности необходимо избегать многочисленных
пересечений работ или стрелок.

10.На СГ не должно быть ни работ, ни событий, имеющих одинаковые
номера или коды.

11.События на СГ нумеруются слева направо и сверху вниз после его
построения и упорядочения следующим образом:

- исходному событию присваивается 0 или 1;

- затем вычеркиваются все выходящие работы из данного события;

- следующий номер можно присвоить такому событию, у которого все
входящие работы вычеркнуты и т. д.;

- если событий, у которых все работы вычеркнуты, окажется
несколько, то нумерация произвольна.