Примеры решения задач.

Пример 1.Триметилгидропероксид 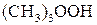реагирует с двухвалентным железом по реакции:

.

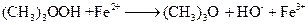Реакция протекает в водном растворе при рН =1. Константа скорости этой реакции при Т=298 К равна 16,4 л/(моль×с), опытная энергия активации 38,6 кДж/моль. Плотность гидропероксида 1,226 г/см³, M = 84 г/моль, плотность раствора, содержащего Fe²⁺, равна 1,2135, М= 56 г/моль. Рассчитать долю активных столкновений из общего числа столкновений, константу скорости данной реакции по теории активных столкновений при Т=298 К и оцените стерический множитель Р.

Р е ш е н и е.

1. Эффективный диаметр столкновений рассчитаем по плотности гидропероксида и раствора железа (+2):

= =

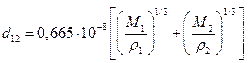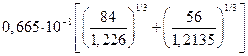=5,099∙10^{-8 см. Откуда: 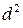= 2,6·10-15}см².

2. Опытная энергия активации связана с теоретической соотношением:

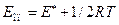. Откуда 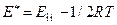= 38600 -0,5×8,314∙298= 37361,214 Дж/моль

3. Доля активных столкновений из общего числа столкновений молекул равна:

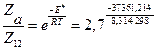= 3,13∙10^-7.

4. Константу скорости по теории активных столкновений рассчитаем по формуле для случая столкновения двух разных молекул:

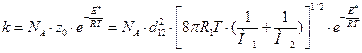[2] см³/(моль·с).

k = 6,022·10²³·2,6·10^-15 =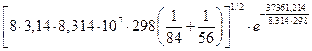

6,67 ×10⁶ 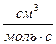=6,67 ×10³ .

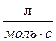5. Стерический множитель Р рассчитаем по формуле: 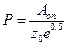, где А_оп – значение предэкспоненциального множителя в уравнении зависимости константы скорости от температуры .

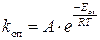Значение предэкспоненциального множителя равно: 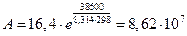л/(моль×с).

Частота стокновений равна: =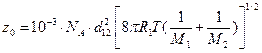

=10^-3·6,022·10²³·2,6·10^-15 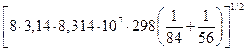= 2,046×10¹⁰ л/(моль×с).

Стерический множитель Р равен:

.

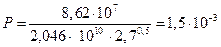Вывод: Реакция взаимодействия триметилгидропероксида с двухвалентным железом относится к бимолекулярным реакциям с валентно-насыщенными молекулами, для которых характерно высокое значение энергии активации и малое значение стерического множителя Р.

Пример 2.

Для элементарной бимолекулярной реакции

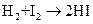
получены опытные значения предэкспоненциального множителя А =1,56·10¹¹(л/моль·с) и энергия активации Е=78,9 Кдж/моль при р⁰= 1 атм. Рассчитайте с помощью теории активированного комплекса при 689 К:

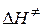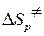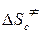а) энтальпию активации ; б) энтропию активации и ; в) энергию Гиббса активации .

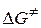Р е ш е н и е. Выскажем предположение, что 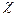=1.

1. Рассчитаем значение константы скорости по формуле:

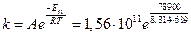=1,79·10⁵ л/моль·с

2. Энтальпия активации 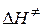связана с опытной энергией активации соотношением:

,

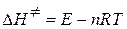где n – молекулярность реакции. В данном случае n=2. Тогда

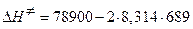=67443,308 Дж/моль.

3. Энтропия активации равна:

=

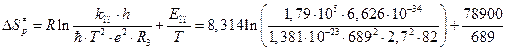= -143,97 Дж/моль×К.

4. Если стандартное состояние С₀ = 1 моль/л, то R₄ =0,082 л∙атм/ моль·К, тогда:

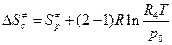= -143,97 + 8,314 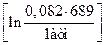= - 110,43 Дж/моль.

5. 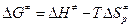=67443,308 -689×(-110,43 )=143529,578 Дж/моль=143,53 кДж/моль.

6. 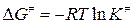; 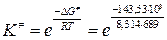=1,55·10^-11.

Вопросы и задания для самоконтроля.

1. В чем заключается основная идея теории активных столкновений?

2. Совпадают ли константа скорости, рассчитанная по теории активных столкновений с константой скорости, определенной из опыта?

3. Физический смысл стерического фактора Р.

4. В чем заключается основная идея теории переходного состояния? Есть ли различие в понятиях «переходное состояние» и «активированный комплекс»?

5. Приведите уравнение, связывающее константу скорости с энтропией активации и опытной энергией активации.

6. Гидролиз метана при температуре 1200 К отвечает кинетике реакции первого порядка. Используя опытные значения энергии активации Е = 335 кДж/моль и значение предэкспоненциального множителя 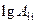=12,2, вычислите при этой температуре энтальпию и энтропию активации реакции.

Глава 5. Катализ

Основные понятия и особенности катализа

Катализ имеет огромное значение в природе и технике. Каталитическими являются процессы синтеза белков и обмен веществ в биологических системах; процессы глубокой переработки нефти с помощью крегинга, гидроочистки, гидрокрегинга и риформинга; синтез и окисление аммиака; производство серной кислоты и метанола; гидролиз сложных эфиров; гидрирование олефинов, и т. д. В настоящее время около 80 % всей химической продукции получается с помощью каталитических процессов.

Каталитические реакции были известны в глубокой древности, однако систематически изучать их начали только в начале прошлого (XXI) века.

Термин ²катализ² ввёл Берцелиус в 1836 г. Современное определение катализа сформулировано в работах Г.К. Борескова.

Катализ –это явление возбуждения химической реакции или изменения их скорости под влиянием веществ – катализаторов, многократно вступающих в промежуточное химическое взаимодействие с участниками реакции и восстанавливающих свой химический состав после каждого цикла промежуточного взаимодействия.

В данном определении подчеркивается, что каталитические процессы имеют химическую природу взаимодействия катализатора и реагента. Однако катализатор – это вещество, поэтому теплота и свет, хотя и влияют на скорость протекания реакции, не являются катализаторам. Катализатор не расходуется в результате химической реакции,

Различные каталитические процессы имеют ряд общих характерных особенностей, связанных в основном с особой ролью катализатора и закономерностями его действия при протекании химических реакций.

При каталитических процессах отсутствуют стехиометрические соотношения между количеством катализатора и реагирующими веществами, так как катализатор во время процесса не расходуется и остаётся химически неизменным. Однако свое физическое состояние катализатор может изменять, например, он может спекаться, отравляться и т. д. Важно отметить, что возможные изменения представляют собой побочные явления, не связанные с его каталитическим действием.

1. Катализатор не влияет на константу равновесия химической реакции, так как стандартное изменение энергии Гиббса процесса (DG) без катализатора и в его присутствии будет одинаковым.

Причина каталитического действия (резкое увеличение константы скорости реакции) связано с изменением механизма реакции в присутствии катализатора по пути, характеризуемом минимальной высотой энергетического барьера. При этом взаимодействие реагента с катализатором переводит вещество в более активную частицу. Речь идет не о переведении реагента в возбужденное состояние, а об образовании нестойкого в условиях реакции нового химического соединения.

Строго говоря, увеличение константы скорости можно объяснить либо уменьшением энергии активации процесса, либо увеличением энтропии активации.

Согласно теории абсолютных скоростей реакций, константа скорости реакции (k) равна:

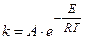, (5.1)

где E = ΔH^* – энергия активации химической реакции или теплота образования активированного комплекса; А – предэкспоненциальный множитель, который определяется из уравнения:

A = A₀ e^DS*/R, (5.2)

или в логарифмической форме

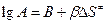, (5.3)

где 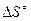– энтропия активации, т.е. энтропия образования активированного комплекса. Энтропия активации при образовании активированного комплекса из исходных веществ с участием катализатора, как правило, существенно уменьшается по сравнению с энтропией активации активированного комплекса в отсутствии катализатора, поскольку присутствие катализатора способствует большей упорядоченности в строении активированного комплекса. Имеются реакции, в которых катализатор почти не влияет на энергию активации, но сильно изменяет предэкспоненциальный множитель (А). Например, реакция гидролиза аденозинтрифосфорной кислоты (АТФ) в присутствии фермента (миозина) ускоряется по сравнению с действием ионов H₃O⁺ в 10¹⁴ раз. Энергия активации процесса при этом практически не изменяется. Для реакции муторации глюкозы в присутствии различных катализаторов энергия активации так же практически не изменяется, предэкспоненциальный множитель(А) изменяется в 10⁶ раз, а константа скорости от 10⁶ до 10⁷ раз. Но такого рода реакции всё-таки более редки.

Более существенно изменение механизма протекания реакции в присутствие катализатора, приводящее к снижению энергии активации реакции.

Так, например, в реакции разложения H₂O₂ в присутствии катализатора (фермента каталазы) энергия активации понижается от 72 до (4¸8) кДж/моль. Это соответствует увеличению скорости реакции в 10²³ раз при постоянстве предэкспоненциального множителя (А). В среднем, энергия активации некаталитических процессов равна 200¸300 кДж.; гетерогенно-каталитических 60¸80 кДж, а ферментативных реакций 30¸40 кДж.

Таким образом, действие катализатора сводится к тому, что из всего многообразия различных путей протекания реакции, катализатор реализует путь с наименьшей высотой активационного барьера.