Термодинамический аспект теории активированного комплекса.

Если константа скорости имеет размерность см³/моль×с и все вещества находятся в стандартном состоянии ( 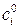=1 моль/см³), то для реакции, протекающей при постоянном объеме:

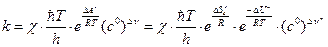. (4.219)

где 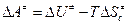– стандартная энергия активации Гельмгольца; 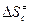– энтропия активации при стандартном состоянии ( 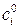=1 моль/см³); 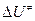– внутренняя энергия активации; 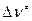= (1-n ) – изменение числа молекул при образовании активированного комплекса; n – число вступающих в реакцию молекул.

Множитель 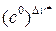в формуле (4.219) необходим, чтобы получить одинаковую размерность в правой и левой частях равенства.

В справочнике физико-химических величин нет значений внутренних энергий активации образования молекул активированного комплекса. Поэтому вместо 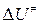при расчетах констант скоростей приходится пользоваться опытными энергиями активации. Чтобы найти связь между этими величинами, прологарифмируем уравнение (4.218)

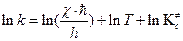, (4.220)

а затем продифференцируем (4.220) по температуре и сравним с уравнением Аррениуса (4.65):

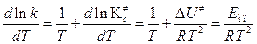. (4.221)

Из сравнения следует, что

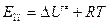(4.222)

Подставив (4.222) в (4.219), получим выражение для константы скорости на основе теории активированного комплекса для реакции, протекающей при постоянном объеме:

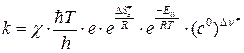. (4.223)

Множитель 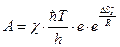равен предэкспоненциальному множителю уравнения Аррениуса, а энтропийный множитель это стерический фактор Р:

Р = 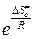. (4.224)

Если реакция протекает в газовой фазе, то в качестве стандартного состояния используют р⁰ = 1 атм. Тогда

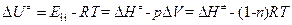. (4.225)

Поэтому энтальпия активации связана с опытной энергией активации соотношением:

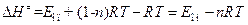. (4.226)

В этом случае для расчета констант из таблиц берут обычно значения энтропии веществ, стандартизованные по давлению, в связи с чем приходится переходить от величин 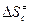к величинам 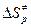. В применении к газовым реакциям будет иметь место соотношение:

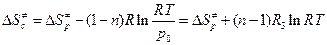, (4.227)

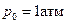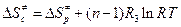Если , то , где R₃ = 82 см³∙атм/моль·К.

Подставив (4.225), (4.227) в уравнение (4.219), получим выражение для расчета константы скорости в случае реакции, протекающей в газовой фазе:

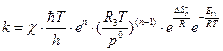см³/моль·с. (4.228)

Из формулы (4.228) нетрудно получить формулу для расчета :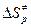

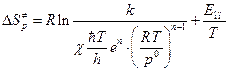Дж/моль×К. (5.36 4.229)

Рассмотрим применение формулы (4.228) к описанию кинетики различных реакций.

1. Для мономолекулярной реакции, в которой образование активированного комплекса происходит без изменения числа частиц (n=1):

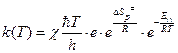. (4.230)

Значение опытной энергии активации (Е) связано с энтальпией активации (n=1) соотношением:

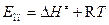. (4.231)

Для мономолекулярных реакций 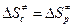, а стерический фактор Р вычисляется по формуле (4.223).

2. В случае бимолекулярной реакции (n=2) из двух молекул газа образуется одна молекула активированного комплекса, поэтому константа скорости может быть вычислена по формуле:

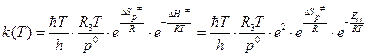. (4.232)

Для бимолекулярной реакции энтальпия активации связана с опытной энергией активации соотношением (р⁰ =1 атм):

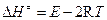. (4.233)

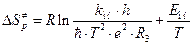. (4.234)

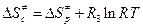. (4.235)

3. Для реакций, протекающих в растворах, константу равновесия 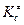выражают через энергию Гельмгольца образования активированного комплекса:

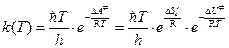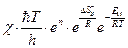= . (4.236)