Стационарное и квазистационарное протекание реакций

Одной из основных задач химической кинетики является установление кинетического уравнения сложной реакции на основе ее механизма. Однако, для математического описания кинетики сложных реакций, включающих несколько параллельно-последовательных стадий с образованием промежуточных веществ, приходится составлять и решать систему дифференциальных уравнений. Решение таких систем чаще всего можно провести только численными методами с использованием ЭВМ.

В химии часто приходится сталкиваться с реакциями, в которых промежуточные частицы обладают столь высокой реакционной способностью, что не могут накапливаться в системе в концентрациях, соизмеримых с концентрациями исходных веществ и продуктов реакции. Такими процессами являются практически все каталитические процессы и процессы, протекающие с участием промежуточных свободных радикалов (радикально-цепные реакции). Важной особенностью процессов, идущих с участием промежуточных частиц, является установление в системе за малый промежуток времени (промежуток времени, в течение которого относительное изменение концентрации исходных веществ невелико) режима, при котором разность скоростей образования 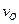и скоростей расходования 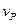промежуточных частиц становится малой по сравнению с самими скоростями. Если поддерживать концентрацию исходных частиц постоянной, то наблюдается равенство скоростей образования и расходования каждой из промежуточных частиц, то есть в системе установится стационарный режим. Такому состоянию системы отвечают стационарные концентрации промежуточных веществ.

Стационарному режиму отвечают условия:

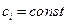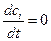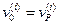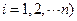; ; ; ( , (4.116)

где n – число промежуточных активных веществ.

Стационарный режим протекания реакции можно установить, например, в реакторе идеального смешения, поддерживая постоянной концентрацию исходного вещества путем непрерывной подачи раствора постоянной концентрации.

Для того, чтобы стационарный режим устанавливался достаточно быстро и затем сохранялся, промежуточные вещества должны быть активными, то есть продолжительность их жизни должна быть небольшой, по сравнению со временем протекания реакции. При этом их концентрации будут достаточно малы.

Метод стационарных концентраций состоит в том, что в системе кинетических уравнений, описывающих сложные химические процессы, скорости по активным частицам принимаются равными нулю.

Это позволяет заменить систему дифференциальных уравнений для концентраций промежуточных частиц алгебраическими уравнениями, выражающими равенство скоростей образования и расходования этих частиц. Таким образом, в кинетических уравнениях для скорости протекания сложной реакции остаются лишь концентрации аналитически определяемых веществ. Система кинетических уравнений существенно упрощается, а решение такой системы облегчается.

Метод кинетического расчета с использованием условия (4.116), при постоянстве концентраций исходных веществ, называется методом стационарных концентраций Боденштейна.

В качестве примера рассмотрим двухстадийную реакцию, состоящую из двух односторонних стадий первого порядка

.

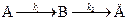Пусть реакция протекает в реакторе идеального смешения, причем концентрация исходного вещества А поддерживается постоянной путем подачи в систему вещества А извне. Через некоторое время после начала реакции в системе установится стационарный режим и концентрация промежуточного вещества В достигнет промежуточного значения 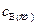, то есть скорость образования вещества В будет равна скорости его расходования.

Тогда, 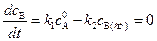. (4.117)

Отсюда 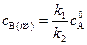. (4.118)

Для стационарного режима легко получить выражение для :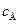

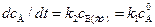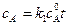, . (4.119)

Таким образом, применение принципа стационарных концентраций для описания данной реакции позволило заменить дифференциальное уравнение для на алгебраическое, чем существенно облегчило решение системы уравнений.

Можно рассчитать через какое время после начала реакции установится стационарный режим. В начальный период реакции скорость образования промежуточного вещества В определяется выражением

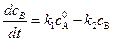. (4.120)

Разделив переменные, получаем:

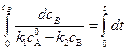. (4.121)

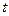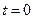
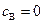Проинтегрировав уравнение (4.121) в пределах от 0 до и от 0 до , приняв, что при , получим:

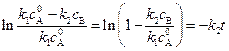, (4.122)

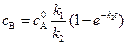. (4.123)

Разделив уравнение (4.123) на (4.118), получим:

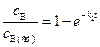. (4.124)

Как следует из уравнения, формально стационарный режим, при котором 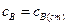будет достигнут только при 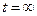. Но если задать достаточно малое, но конечное отклонение 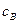от 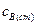, то это отклонение окажется достижимым за достаточно короткое время. Например, будем считать близкой к стационарной концентрацию 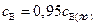. Тогда, из уравнения (4.124) находим

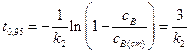. (4.125)

Отсюда, например, при 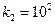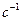, получаем 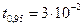с, то есть время достижения стационарного состояния, при достаточно высоких значениях 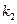, оказывается малым.

При протекании многостадийных реакций в закрытых системах концентрации промежуточных веществ не могут оставаться постоянными, так как концентрации исходных веществ уменьшаются со временем. Однако для достаточно высокоактивных частиц на протяжении всего процесса разность 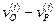остается малой величиной по сравнению с самими значениям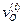и и 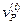и концентрации промежуточных частиц близки к их стационарным значениям, отвечающим составу реакционной смеси в рассматриваемый момент времени. Такой режим называется квазистационарным режимом. Очевидно, что для осуществления квазистационарного режима требование высокой активности промежуточных веществ, непродолжительности их жизни и низкой концентрации имеет еще большее значение, чем при стационарном режиме. Только при этих условиях концентрации промежуточных веществ смогут «подстраиваться» к изменяющейся концентрации исходных веществ в каждый момент времени и принимать значения, требуемые для стационарного протекания процесса. В этом случае можно принять, что 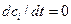, где 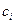- концентрации промежуточных веществ.

Можно оценить время достижения квазистационарного режима на примере реакции

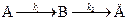
при условии ее протекания в закрытой системе, то есть когда концентрация исходного вещества уменьшается во времени. Кинетика этой реакции описана выше.

Зависимость концентрации исходного вещества А и промежуточного вещества В от времени имеет вид:

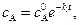(4.126)

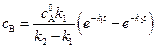. (4.127)

Условие квазистационарности запишется в виде:

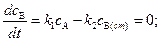
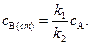(4.128)

Подставив значение 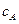из уравнения (4.126) в (4.128), получим:

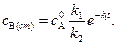(4.129)

Тогда

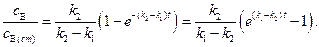(4.130)

Из уравнения (4.130) следует, что при 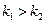отношение 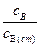при 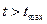больше единицы и увеличивается со временем. То есть квазистационарный режим не может быть осуществлен.

Но при 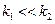можно пренебречь величиной 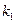в разности 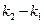и тогда выражение (4.130) переходит в условие (4.124) 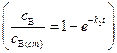для стационарного процесса, то есть квазистационарный режим может быть реализован. В этом случае, выражение для 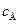можно получить также достаточно легко.

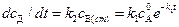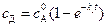, . (4.131)

Если реакция состоит из нескольких последовательных стадий (односторонних и двухсторонних), то квазистационарный режим может быть достигнут только при определенных условиях.