Кинетика последовательных химических реакций
Рассмотрим сложную реакцию, состоящую из двух последовательных стадий первого порядка
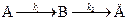
Обозначим текущие концентрации веществ А, В и Д через 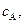
 и
и 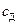 , причем, при
, причем, при 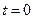 :
: 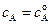 ,
, 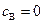 ,
, 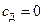 .
.
Кинетику данной реакции можно описать системой трех дифференциальных уравнений:
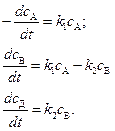 ; (4.104)
; (4.104)
Интегрируя первое, из представленных дифференциальных уравнений, получаем:
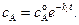 (4.105)
(4.105)
Подставляя выражение для 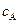 во второе уравнение системы дифференциальных уравнений получаем:
во второе уравнение системы дифференциальных уравнений получаем:
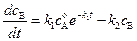 . (4.106)
. (4.106)
Умножив левую и правую часть уравнения (4.106) на 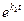 и сгруппировав члены уравнения, получим:
и сгруппировав члены уравнения, получим:
 . (4.107)
. (4.107)
Учитывая, что 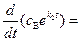
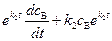 получим:
получим:

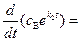
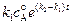 . (4.108)
. (4.108)
При 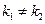 , интегрирование уравнения (4.108) в пределах от 0 до t и от 0 до
, интегрирование уравнения (4.108) в пределах от 0 до t и от 0 до  дает:
дает:
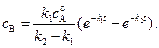 (4.109)
(4.109)
Выражение для концентрации продукта реакции 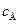 можно найти из дифференциального уравнения скорости его образования или из условия материального баланса –
можно найти из дифференциального уравнения скорости его образования или из условия материального баланса – 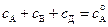 и соотношений (4.105) и (4.109)
и соотношений (4.105) и (4.109)
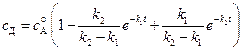 . (4.110)
. (4.110)
На рис 7 приведены зависимости концентраций исходного, промежуточного вещества и конечного продукта от времени для последовательной реакции первого порядка.

Рис. 7. Зависимость концентрации исходного (1), промежуточного (2) вещества и конечного (3) продукта от времени для последовательной реакции первого порядка.
Уравнение кинетической кривой для исходного вещества А совпадает с уравнением для элементарной реакции первого порядка, то есть концентрация вещества А уменьшается с течением времени по экспоненциальному закону.
Кинетическая кривая для вещества В проходит через максимум, координаты которого ( 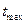 и
и 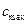 ) можно найти исходя из необходимого требования экстремума
) можно найти исходя из необходимого требования экстремума  . Продифференцируем уравнение (4.109) и приравняем производную к нулю:
. Продифференцируем уравнение (4.109) и приравняем производную к нулю:
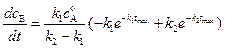 =0 (4.111)
=0 (4.111)
Это условие выполняется, если 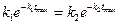 . Отсюда получаем
. Отсюда получаем
 , (4.112)
, (4.112)
где 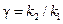 .
.
Чтобы определить, когда концентрация вещества В достигнет максимального значения, подставим (4.112) в (4.109):
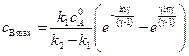 . (4.113)
. (4.113)
Учитывая, что 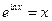 , после преобразований получаем
, после преобразований получаем
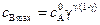 . (4.114)
. (4.114)
Из уравнения (4.114) следует, что максимум концентрации промежуточного вещества В зависит от отношения констант скоростей 
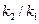 . Можно показать, что с ростом отношения
. Можно показать, что с ростом отношения 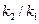 от 0 до
от 0 до 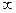 величина
величина 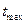 уменьшается от
уменьшается от 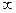 до 0, а
до 0, а 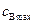 падает от
падает от 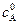 до 0. То есть, максимальная концентрация промежуточного соединения уменьшается и одновременно уменьшается время ее достижения.
до 0. То есть, максимальная концентрация промежуточного соединения уменьшается и одновременно уменьшается время ее достижения.
Зависимость концентрации промежуточного продукта от времени имеет 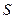 - образную форму. Время, отвечающее точке перегиба на этой зависимости -
- образную форму. Время, отвечающее точке перегиба на этой зависимости -  равно времени достижения максимальной концентрации промежуточного вещества, то есть
равно времени достижения максимальной концентрации промежуточного вещества, то есть 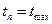 .
.
Накопление вещества Д происходит таким образом, что его концентрация вначале увеличивается медленно, затем все быстрее, а после точки перегиба замедляется. Такой начальный ход кинетической кривой 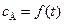 обусловлен тем, что в начальный период реакции, концентрация промежуточного вещества мала, поэтому мала и скорость второй стадии реакции. Этот период реакции называется индукционным. Длительность индукционного периода зависит от соотношения
обусловлен тем, что в начальный период реакции, концентрация промежуточного вещества мала, поэтому мала и скорость второй стадии реакции. Этот период реакции называется индукционным. Длительность индукционного периода зависит от соотношения 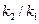 . (Индукционный период может быть обусловлен и другими причинами)
. (Индукционный период может быть обусловлен и другими причинами)
Из полученных кинетических уравнений следует, что концентрация промежуточных веществ и продуктов реакции, 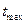 и длительность индукционного периода зависят от соотношения констант скоростей первого и второго периода реакции.
и длительность индукционного периода зависят от соотношения констант скоростей первого и второго периода реакции.
При решении обратной задачи, то есть для нахождения констант скоростей отдельных стадий можно воспользоваться уравнениями кинетических кривых. При этом должны быть определены любые две из трех концентраций, поскольку в закрытой системе они связаны соотношением 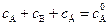 .
.
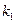 и
и 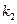 можно также определить с помощью системы кинетических уравнений. Например, с помощью системы уравнений:
можно также определить с помощью системы кинетических уравнений. Например, с помощью системы уравнений:
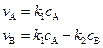 (4.115)
(4.115)
Если определены скорости реакции по двум компонентам А и В как функции концентрации этих компонентов, то 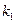 и
и 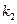 находятся решением системы уравнений. Зависимости
находятся решением системы уравнений. Зависимости  и
и 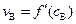 могут быть найдены дифференцированием зависимостей
могут быть найдены дифференцированием зависимостей 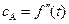 и
и 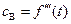 .
.
Дата добавления: 2016-01-09; просмотров: 1934;
