Кинетика химических реакций в реакторе идеального вытеснения
Скорость химической реакции по I-му веществу в реакторе идеального вытеснения с постоянной площадью сечения 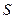 равна:
равна:
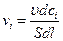 (4.145)
(4.145)
Это уравнение можно проинтегрировать относительно 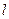 . Тогда
. Тогда
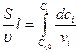 . (4.146)
. (4.146)
Это уравнение позволяет определить изменение концентрации i-го компонента вдоль реактора для реакций любых порядков. Так, например, для реакции первого порядка, протекающей в жидкой фазе ( 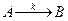 ;
; 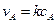 ), получим:
), получим:
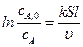 . (4.147)
. (4.147)
Потенцируя полученное уравнение, получим:
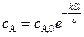 (4.148)
(4.148)
Для реакции второго порядка ( 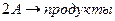 ;
; 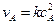 ), получим:
), получим:
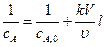 . (4.149)
. (4.149)
Концентрацию вещества А на выходе из реактора можно рассчитать по уравнению (4.146), если вместо 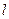 подставить длину реактора
подставить длину реактора 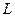 . Тогда, с учетом того, что
. Тогда, с учетом того, что 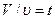 , получим:
, получим:
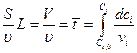 . (4.150)
. (4.150)
Здесь 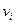 рассчитывается для условий, соответствующих условиям на выходе из реактора. Приведенное уравнение может быть использовано для определения среднего времени пребывания реагента в реакторе и, соответственно, размеров реакционного пространства, а также для определения состава реакционной смеси на выходе из реактора.
рассчитывается для условий, соответствующих условиям на выходе из реактора. Приведенное уравнение может быть использовано для определения среднего времени пребывания реагента в реакторе и, соответственно, размеров реакционного пространства, а также для определения состава реакционной смеси на выходе из реактора.
Тогда, например, для реакции первого порядка:
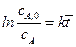 ,
, 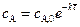 , (4.151)
, (4.151)
Учитывая, что степень превращения вещества А определяется соотношением:
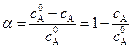
получим
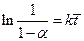 ,
, 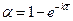 (4.152)
(4.152)
Для параллельной реакции ® 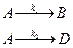 :
:
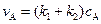 ),
), 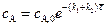 ,
, 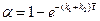 . (4.153)
. (4.153)
При протекании реакций в газовой фазе объем реакционной смеси и соответственно объемная скорость 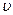 может изменяться по мере ее движения в реакторе. Это изменение нужно учитывать при выводе кинетических уравнений.
может изменяться по мере ее движения в реакторе. Это изменение нужно учитывать при выводе кинетических уравнений.
Рассмотрим, например, реакцию:
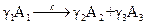 ,
,
протекающую в газовой фазе. Так как объемная скорость в уравнении (4.145) является постоянной величиной, то введя ее под знак дифференциала получаем:
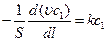 , (4.154)
, (4.154)
где 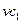 - количество молей вещества
- количество молей вещества 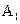 , проходящее через любое сечение реактора в единицу времени. Обозначив
, проходящее через любое сечение реактора в единицу времени. Обозначив 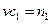 , выразим
, выразим 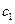 через
через 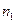 , тогда
, тогда
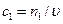 . (4.155)
. (4.155)
Если реакционная смесь является идеальным газом, то
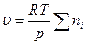 , (4.156)
, (4.156)
где 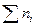 - общее количество молей всех веществ, проходящих через сечение реактора в единицу времени.
- общее количество молей всех веществ, проходящих через сечение реактора в единицу времени.
Тогда
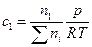 . (4.157)
. (4.157)
Если в реактор в единицу времени поступает начальное количество 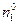 молей вещества
молей вещества 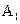 , то на некотором расстоянии от начала реактора прореагирует доля этого вещества
, то на некотором расстоянии от начала реактора прореагирует доля этого вещества 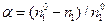 , называемая степенью превращения вещества
, называемая степенью превращения вещества 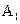 . Отсюда
. Отсюда
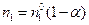 . (4.158)
. (4.158)
Для данного сечения реактора количество вещества 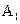 , проходящего в единицу времени через реактор, равно
, проходящего в единицу времени через реактор, равно 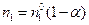 ; количество вещества
; количество вещества 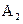 равно -
равно - 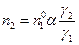 ; количество вещества
; количество вещества 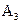 равно
равно 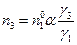 . Суммируя количества всех веществ, получим:
. Суммируя количества всех веществ, получим:
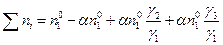 . (4.159)
. (4.159)
Преобразовав это уравнение, получим
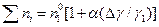 , (4.160)
, (4.160)
где 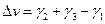 .
.
Подставив (4.158) и (4.160) в (4.157), имеем:
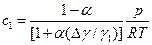 . (4.161)
. (4.161)
Так как
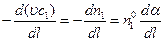 , (4.162)
, (4.162)
То, подставив (4.161) в (4.154), получим:
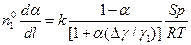 . (4.163)
. (4.163)
Так как температура и давление не изменяются вдоль реактора, то, разделив переменные в уравнении (4.163) и проинтегрировав в пределах от 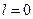 до
до 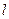 и, соответственно, от
и, соответственно, от 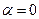 до
до 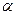 , получим:
, получим:
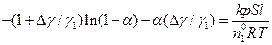 . (4.164)
. (4.164)
Это уравнение выражает в неявном виде изменение степени превращения 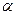 вдоль оси реактора.
вдоль оси реактора.
Если 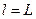 , а
, а 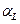 - степень превращения на выходе из реактора, то
- степень превращения на выходе из реактора, то
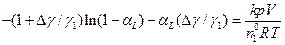 . (4.165)
. (4.165)
Уравнение (4.165) позволяет рассчитать степень превращения 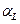 при заданной скорости подачи вещества
при заданной скорости подачи вещества 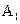 в реактор, если известна величина константы скорости реакции.
в реактор, если известна величина константы скорости реакции.
Пример 1. В реакторе идеального смешения происходят следующие реакции
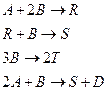
где 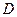 целевой продукт реакции.
целевой продукт реакции. 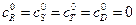 .
.
Начальная концентрация исходного вещества А: 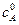 = 1 кмоль/ м3. Текущие концентрации веществ:
= 1 кмоль/ м3. Текущие концентрации веществ: 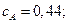
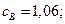
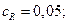
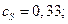
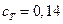 кмоль/
кмоль/ 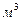 .
.
Скорость подачи исходных веществ 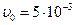
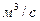 .
.
Определить производительность реактора по веществу В и по веществу D.
Р е ш е н и е.
Производительность реактора по веществу В равна 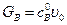 , а по веществу D –
, а по веществу D – 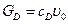 . Неизвестные концентрации
. Неизвестные концентрации 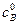 и
и 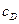 можно определить из уравнения материального баланса.
можно определить из уравнения материального баланса.
Составим уравнение материального баланса для реактора идеального смешения.
На основании стехиометрических соотношений реакций запишем:
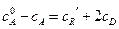 ;
; 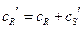 ;
; 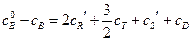 ;
; 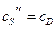 ;
; 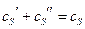 ,
,
где 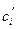 - промежуточные концентрации веществ.
- промежуточные концентрации веществ.
Комбинируя полученные уравнения, получим:
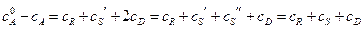 ;
;
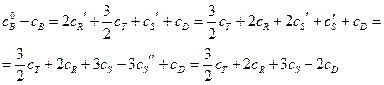
Определим 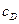 :
:
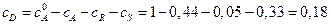 кмоль/м
кмоль/м 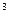 .
.
Производительность реактора по веществу D равна
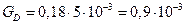 кмоль/с.
кмоль/с.
Определим 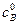 :
:
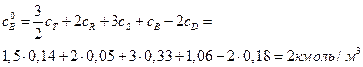
Производительность реактора по веществу 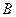 равна
равна
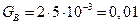 кмоль/с.
кмоль/с.
Пример 2. Установка состоит из следующих последовательно соединенных реакторов:
идеального смешения ( 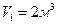 ), идеального вытеснения (
), идеального вытеснения ( 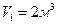 ) и идеального смешения (
) и идеального смешения ( 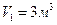 ). Начальная концентрация вещества
). Начальная концентрация вещества 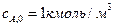 , скорость подачи
, скорость подачи 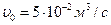 . В реакторах протекает реакция первого порядка
. В реакторах протекает реакция первого порядка 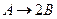 . Константа скорости реакции
. Константа скорости реакции 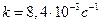 . В начальный момент времени продукт в системе отсутствует, плотность реакционной системы в ходе реакции не меняется.
. В начальный момент времени продукт в системе отсутствует, плотность реакционной системы в ходе реакции не меняется.
Определить концентрацию исходного вещества после каждого реактора и рассчитать производительность установки по продукту.
Р е ш е н и е.
1. Составим материальный баланс для первого и третьего реакторов и решим кинетическое уравнение реакции для реактора идеального вытеснения, если известно время пребывания вещества в реакторе 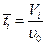 .
.
Составим материальный баланс по веществу 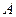 для первого реактора.
для первого реактора.
Для стационарного процесса 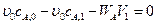 .
.
Отсюда 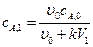 =
= 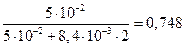 кмоль/м3.
кмоль/м3.
2. Время пребывания вещества в реакторе идеального смешения для реакции первого порядка равно:
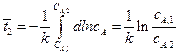 .
.
Отсюда:
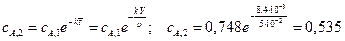
3. Для третьего реактора идеального смешения материальный баланс запишется:
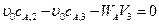 .
.
Тогда 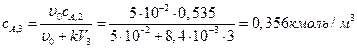 .
.
4. Производительность системы по продукту 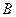 :
:
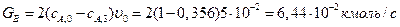 .
.
Дата добавления: 2016-01-09; просмотров: 1959;
