Кинетика химических реакций в реакторе идеального смешения
Уравнения, описывающие зависимость концентрации компонентов в реакторе идеального смешения существенно сложнее, чем в закрытой системе. Как уже отмечалось, в открытых системах производная от концентрации по времени не является скоростью реакции. Кроме того, уравнение материального баланса не может быть непосредственно выведено из стехиометрического уравнения. Приведем вывод некоторых основных соотношений, описывающих протекание реакций простых типов в реакторе идеального смешения.
Пусть в реактор, объем которого 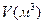 , вводится реакционная смесь с объемной скоростью
, вводится реакционная смесь с объемной скоростью 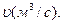 Одновременно, из реактора выводится реакционная смесь с той же объемной скоростью. При этом объем реакционного пространства будет оставаться постоянным.
Одновременно, из реактора выводится реакционная смесь с той же объемной скоростью. При этом объем реакционного пространства будет оставаться постоянным.
В результате интенсивного перемешивания концентрация в любой точке реактора одинакова и не меняется во времени. При входе в реактор концентрация вещества уменьшается скачком. Концентрация реакционной смеси выходящей из реактора такая же, как в любой точке реакционного пространства.
Количество i-го вещества, которое вводится в реактор, в единицу времени с конвективным потоком будет равно 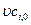 (кмоль/с). За это же время из реактора с конвективным потоком выводится количество i-го вещества равное
(кмоль/с). За это же время из реактора с конвективным потоком выводится количество i-го вещества равное 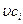 . Расход (образование) i-го вещества в ходе химической реакции составит
. Расход (образование) i-го вещества в ходе химической реакции составит 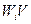 (кмоль/с). Тогда
(кмоль/с). Тогда
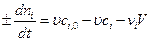 . (4.132)
. (4.132)
Если скорость химической реакции определяется по исходному веществу, то ставится знак (-), а если по продукту реакции – то ставится знак (+). Скорость химической реакции должна определяться при условиях соответствующих условиям на выходе из реактора.
Полученное уравнение описывает зависимость концентрации реагентов в реакторе идеального смешения для реакций любых порядков.
Рассмотрим кинетику реакций в реакторе идеального смешения на примере реакции первого порядка
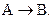
Для данной реакции запишем уравнение материального баланса по веществу А. Так как для реакции первого порядка 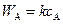 , то уравнение материального баланса будет иметь вид
, то уравнение материального баланса будет иметь вид
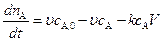 ,
,
или 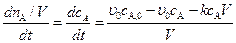 . (4.133)
. (4.133)
Разделив переменные, получим:
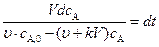 . (4.134)
. (4.134)
Интегрирование этого уравнения в пределах от 0до t и от 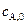 до
до 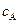 дает:
дает:
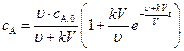 . (4.135)
. (4.135)
Уравнение зависимости концентрации вещества В от времени протекания реакции можно вывести из уравнения материального баланса по веществу В. Если в поступающем в реактор растворе отсутствует вещество В, то есть 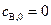
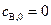 , то, с учетом того, что
, то, с учетом того, что 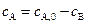 , уравнение материального баланса запишется:
, уравнение материального баланса запишется:
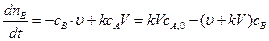 . (4.136)
. (4.136)
Решив это дифференциальное уравнение, получим:
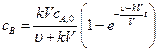 . (4.137)
. (4.137)
Это уравнение можно получить так же из соотношения: 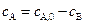 .
.
Из уравнений (4.135) и (4.137) следует, что при 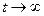 концентрации А и В достигают предельных постоянных значений. Это означает, что сумма скоростей расходования вещества А за счет химической реакции и за счет ухода из реактора вместе с реакционной смесью становится равной скорости его поступления в реактор. Для вещества В установление постоянной концентрации означает, что скорость его накопления в результате образования из вещества А становится равной скорости его ухода из реактора. Такой режим процесса называется стационарным режимом, а концентрации А и В, соответствующие этому режиму, называются стационарными:
концентрации А и В достигают предельных постоянных значений. Это означает, что сумма скоростей расходования вещества А за счет химической реакции и за счет ухода из реактора вместе с реакционной смесью становится равной скорости его поступления в реактор. Для вещества В установление постоянной концентрации означает, что скорость его накопления в результате образования из вещества А становится равной скорости его ухода из реактора. Такой режим процесса называется стационарным режимом, а концентрации А и В, соответствующие этому режиму, называются стационарными: 
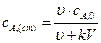 ;
; 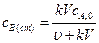 . (4.138)
. (4.138)
Установление стационарного режима является важнейшей особенностью процессов, протекающих в открытых системах при постоянной скорости массопереноса.
Нахождение стационарных концентраций может быть выполнено без интегрирования уравнений, путем приравнивания нулю производной от концентраций компонентов реакционной смеси от времени. То есть:
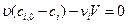 . (4.139)
. (4.139)
Используя это уравнение легко получить выражения для стационарных концентраций компонентов для реакций любых порядков.
Следует отметить, что время достижения состояния, близкого к стационарному, может оказаться весьма малым. Близким к стационарному можно считать состояние, когда отклонение текущей концентрации от стационарной не превышает 5%. Тогда, например 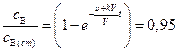 . При
. При 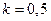
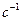 ,
, 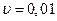
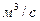 и
и 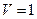
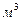 время достижения стационарного состояния будет равно 5,87 с.
время достижения стационарного состояния будет равно 5,87 с.
Степень превращения компонентов зависит от скорости химической реакции и от времени пребывания реакционной смеси в реакторе. Среднее время пребывания реакционной смеси в реакторе определяется объемом реактора и объемной скоростью подачи реагентов в реактор: 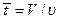 . Как правило,
. Как правило, 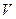 и
и 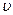 варьируются таким образом, чтобы среднее время пребывания реакционной смеси в реакторе было больше или равно (с определенным приближением) времени наступления стационарного режима. Тогда
варьируются таким образом, чтобы среднее время пребывания реакционной смеси в реакторе было больше или равно (с определенным приближением) времени наступления стационарного режима. Тогда
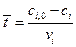 . (4.140)
. (4.140)
Отсюда, для реакции первого порядка ( 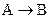 ) эти величина равны:
) эти величина равны:
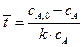 ;
; 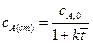 ;
; 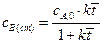 . (4.141)
. (4.141)
Для решения практических задач удобно концентрации реагентов выражать через степень превращения вещества ( 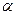 ). Так как
). Так как 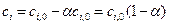 , то
, то 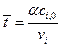 .
.
Тогда, для реакции первого порядка:
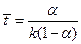 a
a 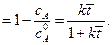 (4.142)
(4.142)
Для реакции второго порядка ( 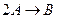 ):
):
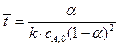 , (4.143)
, (4.143)
для параллельной реакции ( 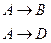 ) :
) :
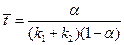 . (4.144)
. (4.144)
Эти уравнения позволяют, при заданных объеме и производительности по исходному веществу, определить концентрацию реагентов на выходе из реактора или среднее время пребывания 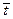 и, затем, размеры реакционного пространства
и, затем, размеры реакционного пространства 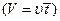 при заданной степени химического превращения.
при заданной степени химического превращения.
Часто скорость сложных химических реакций выражается в виде кинетических уравнений дробного порядка. В этом случае аналитическое решение оказывается невозможным и приходится прибегать к численным или графическим методам решения.
Дата добавления: 2016-01-09; просмотров: 1513;
