Кинетика двусторонних (обратимых) химических реакций
1. Рассмотрим двустороннюю (обратимую) реакцию
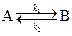 ,
,
протекающую в закрытой системе при постоянном объеме, когда обе стадии, прямая и обратная, являются реакциями первого порядка. Если скорости прямой и обратной реакций в изучаемом диапазоне условий соизмеримы, то, согласно закону действующих масс, выражение для суммарной скорости записывается в виде разности скоростей прямой и обратной реакций.
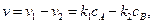 (4.69)
(4.69)
откуда

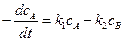 . (4.70)
. (4.70)
Пусть начальные концентрации веществ А и В равны соответственно 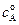 и
и 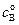 , а количество прореагировавшего вещества А в единице объема, то есть уменьшение концентрации вещества А к моменту времени t равно х. Из условия материального баланса можно записать
, а количество прореагировавшего вещества А в единице объема, то есть уменьшение концентрации вещества А к моменту времени t равно х. Из условия материального баланса можно записать 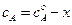 и
и 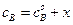 . После введения этих обозначений, уравнение (4.70) можно записать в следующем виде:
. После введения этих обозначений, уравнение (4.70) можно записать в следующем виде:
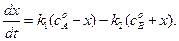 (4.71)
(4.71)
Преобразуя уравнение (4.71), получим:
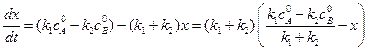 . (4.72)
. (4.72)
В момент равновесия ( 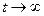 ) скорость двусторонней реакции будет равна нулю, то есть
) скорость двусторонней реакции будет равна нулю, то есть 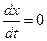 и
и 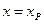 , где
, где 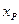 - количество вещества А в единице объема, прореагировавшего к моменту установления равновесия. Тогда
- количество вещества А в единице объема, прореагировавшего к моменту установления равновесия. Тогда 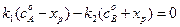 , откуда
, откуда
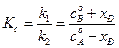 , (4.73)
, (4.73)
где Kс –константа равновесия реакции. Решив уравнение (4.73) относительно 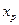 получим соотношение:
получим соотношение:
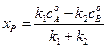 . (4.74)
. (4.74)
Подставив (4.74) в (4.72) получим:
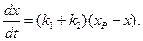 (4.75)
(4.75)
Разделяя переменные и интегрируя от 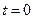 до
до 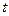 и от
и от 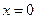 до
до 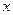 получим:
получим:
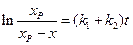 и (4.76)
и (4.76)
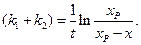 (4.77)
(4.77)
Уравнение (4.77) аналогично уравнению (4.24) для односторонней реакции первого порядка, с той лишь разницей, что вместо 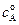 и
и 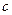 , в нем фигурируют соответственно
, в нем фигурируют соответственно 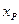 и
и 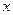 , а в качестве кинетического параметра – сумма констант скоростей
, а в качестве кинетического параметра – сумма констант скоростей 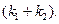
Количество вещества, вступившего в реакцию к моменту времени t можно рассчитать, по соотношению:
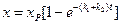 . (4.78)
. (4.78)
Изменение концентрации реагентов и продуктов реакции во времени можно изобразить на графике (рис 6).
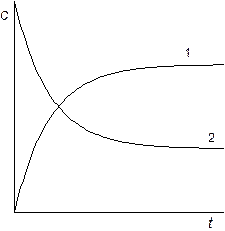
Рис. 6 Зависимость концентрации реагентов от времени
Для обратимой реакции первого порядка.1 – продукт реакции, 2 –исходное вещество.
Выражение (4.78)можно также представить в виде уравнения прямой линии:
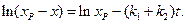 (4.78)
(4.78)
Таким образом, для обратимой реакции первого порядка должна соблюдаться линейная зависимость функции 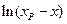 от времени. Из значения тангенса угла наклона прямой можно вычислить сумму констант скоростей прямой и обратной реакций –
от времени. Из значения тангенса угла наклона прямой можно вычислить сумму констант скоростей прямой и обратной реакций – 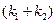 .
.
Для расчета значений каждой из констант, необходимо рассчитать константу равновесия реакции 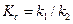 из термодинамических (можно справочных) данных или по формуле (4.73):
из термодинамических (можно справочных) данных или по формуле (4.73):
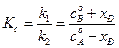
Зная значения 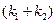 и
и 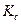 , нетрудно рассчитать каждую из констант отдельно:
, нетрудно рассчитать каждую из констант отдельно:
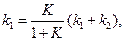
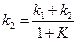 . (4.79)
. (4.79)
2. Типичным примером обратимой химической реакции, в которой обе реакции протекают как реакции второго порядка, является реакция омыления сложного эфира
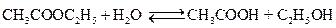
Схема такой реакции
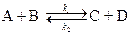
Решение задачи рассмотрим для случая, когда продукты реакции до начала реакции в реакционной смеси отсутствуют: СА0= СВ0=а.
Уравнение скорости химической реакции можно записать в виде:
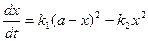 . (4.80)
. (4.80)
При достижении состояния равновесия выполняется условие:
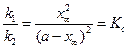 . (4.81)
. (4.81)
С учетом уравнения (4.81) уравнение (4.80) для скорости химической реакции запишется как:
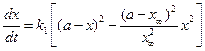 . (4.82)
. (4.82)
Полином допускает наличие двух корней квадратного уравнения х1= х∞ и х2= 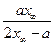 , его записывают через произведение вида: m(х-х1) (х-х2). Уравнение скорости химической реакции запишется как:
, его записывают через произведение вида: m(х-х1) (х-х2). Уравнение скорости химической реакции запишется как:
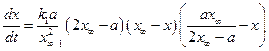 . (4.83)
. (4.83)
Интегральная форма этого уравнения имеет вид
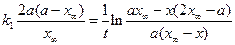 . (4.84)
. (4.84)
Константы скоростей k1 и k2можно определить из опытного значения кажущейся константы скорости:
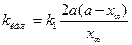 и
и 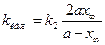 . (4.85)
. (4.85)
Дата добавления: 2016-01-09; просмотров: 2892;
