Кинетика односторонних химических реакций второго порядка
Случай 1. Когда в элементарном акте реагируют две одинаковые частицы или когда концентрации исходных веществ А1 и А2 равны:
2А ®продукты или А1+А2 ®продукты.
Запишем выражение для скорости:
1) по закону действующих масс: v = k¢×C2;
2) из определения скорости реакции: v =  .
.
При выводе уравнения константы скорости химической реакции, приравняем полученные выражения, разделим переменные и проинтегрируем, учитывая что  :
:
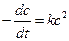 ,
, 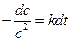 ,
, 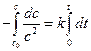 ,
,
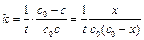 , (4.33)
, (4.33)
Размерность константы скорости реакции второго порядка – «время -1×концентрация-1». Например: л/(моль×с).
Зависимость концентрации от времени выражается уравнением
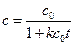 . (4.34)
. (4.34)
Кинетическое уравнение для реакции второго порядка, согласно уравнению (1.19) имеет вид:
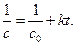 (4.35)
(4.35)
Откуда следует, что график в координатах  – есть уравнение прямой с тангенсом угла наклона
– есть уравнение прямой с тангенсом угла наклона 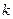 .
.
Период полупревращения для реакции второго порядка равен:
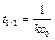 . (4.36)
. (4.36)
Как видно из этого уравнения, период полупревращения для реакции второго порядка обратно пропорционален начальной концентрации реагента.
Случай 2. Концентрации исходных веществ разные:
А1 + А2 ®продукты
Пусть начальные и текущие концентрации веществ 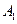 и
и 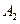 равны соответственно:
равны соответственно:
 ,
, 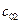 ,
, 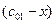 и
и 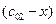 , где
, где  - текущее изменение концентрации.
- текущее изменение концентрации.
Запишем выражение для скорости:
1) по закону действующих масс
v = k× (с01– x) (с02 – x); (4.37)
2) из определения скорости реакции
v = 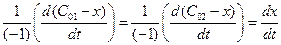 (4.38)
(4.38)
Для нахождения константы скорости химической реакции прировняем уравнения (4.37 и 4.38) друг другу, разделим переменные и проинтегрируем:
 . (4.39)
. (4.39)
Как видно из уравнения (4.39), размерность константы скорости реакции второго порядка – «время -1×концентрация-1».
Дата добавления: 2016-01-09; просмотров: 1649;
