Колебания в системах с медленно изменяющимися параметрами.

В качестве примера такой системы можно снова рассмотреть маятник с переменной длиной при выполнении условия

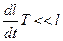. (1)

Условие (1) означает, что длина маятника мало изменяется за период колебаний .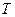

Такие изменения параметров колебательной системы называются адиабатическими.

Рассмотрим гармонический осциллятор, описываемый уравнением

,

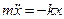у которого коэффициент адиабатически изменяется со временем. В этом случае полная энергия 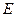зависит от времени. Вычислим производную от 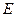по :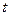

.

При этом движение имеет характер колебаний с медленно изменяющимися периодом и амплитудой. Будем считать, что величина 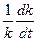также изменяется медленно. Тогда ее можно представить в виде:

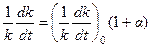
Индекс “0” означает, что значение величины в скобках берется в середине периода колеба-ний. Малая поправка 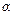является величиной более высокого порядка малости, чем .

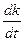Тогда изменение энергии осциллятора за период колебаний

.

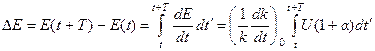Отбросим в этом выражении 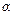и индекс “0” у множителя перед интегралом. Это приведет к ошибке 2 – го порядка малости по 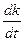. В силу периодичности решения можно положить . Тогда получим

. (2)

Полагая 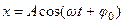и проводя интегрирование в выражении (2), находим

.

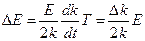Считая, что 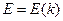, приходим к уравнению

.

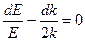Интегрируя и учитывая, что 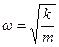, получим

, , или , .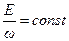

Таким образом, при адиабатическом изменении параметров колебательной системы существуют функции ее параметров, которые остаются постоянными. Такие функции называются адиабатическими инвариантами.

Адиабатические инварианты являются эффективным средством исследования колебатель-ных систем различной природы. Они широко использутся в терии ускорителей заряженных частиц, в физике плазмы, в атомной физике и т. д.

Пример. Движение заряенной частицы в неоднородном магнитном поле.

Заряженная частица с зарядом , как известно из школьного курса физики, движется в магнитном поле по винтовой линии вдоль направления вектора индукции 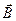(рис. 1).

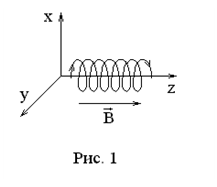
На частицу действует сила Лоренца

,

которая изменяет лишь направление скорости частицы, оставляя неизменной ее кинетическую энергию.

Разложим вектор скорости на составляющие вдоль 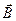и перпендикулярно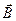

.

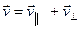В плоскости, перпендикулярной к 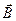второй закон Ньютона имеет вид:

, отсюда (ларморовский радиус).

Таким образом, в плоскости частица вращается по окружности радиуса 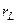с угловой скоростью 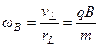(ларморовская частота). В продольном направлении сила Лоренца не влияет на движение частицы, то есть .

В проекции на ось 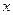уравнение движения приводится к уравнению осциллятора

.

Рассмотрим теперь движение заряженной частицы в неоднородном магнитном поле , . В этом случае, если за период вращения в плоскости магнит-ное поле изменяется мало, то его изменение является адиабатическим. В этом случае, как было показано выше существует адиабатический инвариант

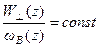, где - кинетическая энергия поперечного движения.

Обычно при рассмотрении таких движений в качестве адиабатического инварианта выбирается магнитный момент

.

Из этого соотношения следует, что при движении в сторону усиливающегося магнитного поля поперечная энергия частицы возрастает. При этом, так как , сохраняется полная энергия , где 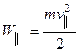. Значит при возрастании должна убывать продольная энергия 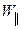, то есть частица будет тормозится в нарастающем магнитном поле. В момент, когда 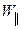обратится в нуль, произойдет отражение частицы от области сильного магнитного поля. Поэтому в физике плазмы такие области называют магнитными зеркала-ми, или магнитными пробками. Это явление используется для удержания горячей плазмы в магнитных ловушках (пробкотронах). Аналогичный характер имеет движение заряженных частиц в магнитном поле Земли. В этом случае, частицы отражаются от областей более сильного поля в области полюсов.

ЛЕКЦИЯ 15