Параметрический резонанс. Автоколебания.

Параметрическое возбуждение колебаний – один из параметров колебательной системы периодически изменяется со временем с частотой 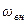. Оно проявляется в известном всем нам с детства процессе. Человек, стоя на качелях, может сам себя раскачать, перодически приседая и поднимаясь во весь рост с частотой в два раза большей собственной частоты такого физического маятника.

Простой пример: маятник с переменной длиной.

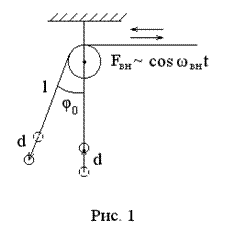
Будем считать, что при прохождении положения равновесия длина маятника уменьшается на величину 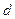( 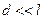) , а в крайнем положении – увеличивается на то же значение. В среднем за период колебаний длина маятника остается неизменной. Такое измене-ние длины соответствует условию

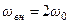, (1)

где 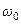- собственная частота.

Рост энергии колебаний со временем объясняется тем, что опускание маятника происходит в наклон-ном положении и работа внешней силы за каждое подтягивание и опускание равна

( ).

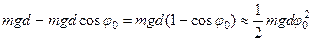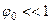Полная работа внешней силы за период колебаний

.

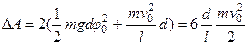Здесь 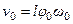- скорость маятника в нижнем положении. Второе слагаемое в скобках учитывает дополнительную работу для создания нормального ускорения .

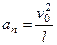В силу того, что 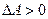энергия маятника постоянно возрастает. Учитывая малость 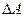можно записать

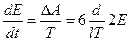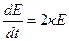, или , где .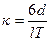

Решение этого дифференциального уравнения имеет вид:

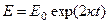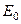, - начальная энергия.

Таким образом, при выполнении условия (1) энергия колебаний экспоненциально растет со временем. Это явление называется параметрическим резонансом. При наличии трения энергия экспоненциально умеьшается со временем по закону

.

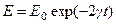Сравнивая два последних выражения, получаем, что параметрический резонанс имеет место при условии 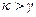. Величина 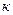пропорциональна амплитуде колебаний длины маятника 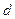. Следовательно, параметрический резонанс, в отличие от обычного резонанса, рассмотрен-ного в лекции 12, может возникать лишь при амплитуде, превышающей некоторое пороговое значение.

Параметрические колебания играют очень важную во многих физических системах (генера-торы электромагниных колебаний, установки с лазерным термоядерным синтезом и т. д.).

Рассмотренные два типа незатухающих колебаний существуют благодаря постоянному вводу энергиии в колебательную систему за счет работы внешних сил. Существует еще один важный тип незатухающих колебаний – автоколебания. В этом случае система сама регули-рует поступление энерги от некоторого источника для компенсации потерь на трение. Это осуществляется с помощью некоторого устройства, управляемого посредством обратой связи с колебательной системой.

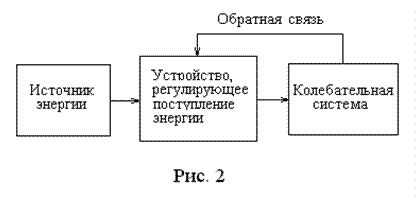
В отличие от свободных колебаний, амплитуда автоколебаний определяется не начальными условиями, а свойствами самой системы. Примеры механических автоколебаний: механи-ческие часы, колебания струны под действием смычка, движение поршня паровой машины и т.д. Важным частным случаем автоколебаний являются так называемые релаксационные колебания, при которых в системе в течение длительного времени накапливаются измене-ния, а затем происходит резкий переход в первоначальное состояние.

ЛЕКЦИЯ 14