Работа и энергия. Закон сохранения энергии.

Работа силы 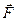 на пути
на пути  :
:
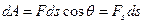 ,
,  - проекция
- проекция 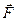 на
на  ,
,
 при
при 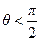 ,
,  при
при 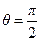 ,
,
 при
при  .
.
Скалярное произведение векторов 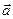 и
и  :
: 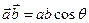 ,
,  - угол между векторами.
- угол между векторами.
Скалярное произведение можно выразить через проекции:  .
.
Тогда элементарную работу можно записать в виде:
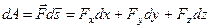 .
.
Работа силы на конечном пути
Разбивая траекторию движения материальной точки на последовательность малых переме-щений 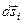 , можно представить работу силы
, можно представить работу силы 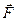 на конечном пути
на конечном пути  от точки 1 до точки 2 в виде:
от точки 1 до точки 2 в виде:
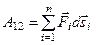 или в пределе при
или в пределе при 
 .
.
Мощность:  (работа в единицу времени). Часто бывает удобно выражать работу через силу и скорость:
(работа в единицу времени). Часто бывает удобно выражать работу через силу и скорость:
 или
или  .
.
Силовое поле – совокупность всех сил, действующих на данную материальную точку в любой точке пространства.
Потенциальное силовое поле – работа сил в таком поле при перемещении материальной точки не зависит от формы пути. Примеры: гравитационное поле, электростатическое поле.
Консервативные силы – силы, действующие в потенциальном силовом поле.
Некосервативные силы – работа зависит от формы пути (например, сила трения).
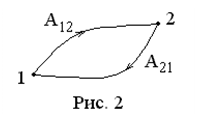
Работа консервативных сил при перемещении материаль-ной точки по замкнутому контуру равна нулю.Для консер-вативных сил  (см. рис. 2), следовательно,
(см. рис. 2), следовательно,
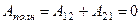 .
.
Потенциальная энергия U – функция, изменение которой при перемещении материальной точки равно работе консервативной силы 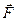 , взятой с обратным знаком
, взятой с обратным знаком
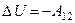 . (1)
. (1)
Из этого определения видно, что потециальная энергия определена с точностью до произ-вольной константы. Например, в выражении для потенцильной энергии тела в поле тяжести вблизи поверхности Земли 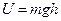 по этой причине высоту
по этой причине высоту 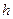 можно отсчитывать от любого уровня. При вычислении работы по формуле (1) произвольная константа сокращает-ся. Для того чтобы вычислять значение самой потенциальной энергии удобно зафиксировать значение соответствующей константы. Это можно сделать по разному. Например, в электро-статике потенциал поля точечного заряда на бесконечности считается равным нулю. Можно, задать равным нулю значение
можно отсчитывать от любого уровня. При вычислении работы по формуле (1) произвольная константа сокращает-ся. Для того чтобы вычислять значение самой потенциальной энергии удобно зафиксировать значение соответствующей константы. Это можно сделать по разному. Например, в электро-статике потенциал поля точечного заряда на бесконечности считается равным нулю. Можно, задать равным нулю значение  в начале координат. Тогда определение потенциальной энергии можно сформулировать следующим образом.
в начале координат. Тогда определение потенциальной энергии можно сформулировать следующим образом.
 Потенциальная энергия равна работе сил потенциального поля при перемещении материальной точки из начала координат в данную точку, взятой с обратным знаком.
Потенциальная энергия равна работе сил потенциального поля при перемещении материальной точки из начала координат в данную точку, взятой с обратным знаком.
Тогда
 ,
, 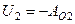 ,
, 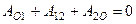 ,
,
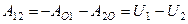 , значит
, значит
 . (2)
. (2)
Рассмотрим бесконечно малое перемещение 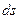 между двумя близкими точками
между двумя близкими точками 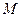 и
и 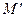 .
.
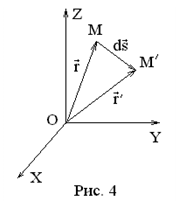
 ,
,  .
.
Тогда  . (3)
. (3)
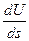 - производная по направлению (градиент ).
- производная по направлению (градиент ).
Для проекций 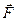 имеем:
имеем:
 ,
,  ,
, 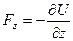 .
.
В качестве примера использования этих формул вычислим потенциальную энергию материальной точки под действием упругой силы. По закону Гука 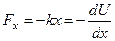 . Отсюда
. Отсюда 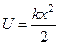 .
.
Кинетическая энергия материальной точки
Рассмотрим движение материальной точки под действием произвольной силы 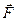 . По второму закону Ньютона
. По второму закону Ньютона
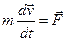 . Тогда
. Тогда 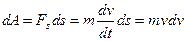 или
или  .
.
Величина 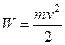 называется кинетической энергией тела. Значит
называется кинетической энергией тела. Значит
 ,
,
то есть работа силы 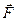 равна изменению кинетической энергии тела. Для консервативной силы
равна изменению кинетической энергии тела. Для консервативной силы
 .
.
Величина 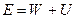 называется полной энергией материальной точки. Тогда в потенци-альном поле имеет место закон сохранения энергии
называется полной энергией материальной точки. Тогда в потенци-альном поле имеет место закон сохранения энергии
 или
или  .
.
Закон сохранения энергии выполняется и для замкнутой системы материальных точек:
 ,
,
где 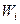 - кинетическая энергия
- кинетическая энергия 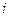 -ой точки,
-ой точки, 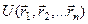 - потенциальная энергия взаимо-действия материальных точек системы.
- потенциальная энергия взаимо-действия материальных точек системы.
Изменение энергии под действием неконсервативных сил
Рассмотрим движение материальной точки под дейсвием двух сил: консервативной силы 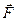 и неконсервативной силы
и неконсервативной силы  . Тогда работа суммарной силы
. Тогда работа суммарной силы 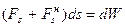 . Для кон-сервативной силы
. Для кон-сервативной силы  . Тогда
. Тогда 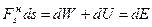 . Для работы на конечном пути получим
. Для работы на конечном пути получим
 .
.
Таким образом, работа неконсервативной силы равна изменению полной энергии материаль-ной точки.
Единицы измерения работы энергии и мощности
СИ: 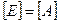 = 1 Нּм = 1 Джоуль,
= 1 Нּм = 1 Джоуль, 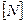 = 1 Джоуль/сек = 1 Ватт.
= 1 Джоуль/сек = 1 Ватт.
СГС:  = 1динаּсм = 1 эрг, 1 Джоуль = 107 эрг,
= 1динаּсм = 1 эрг, 1 Джоуль = 107 эрг, 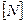 = 1 эрг/сек.
= 1 эрг/сек.
ЛЕКЦИЯ 6
Упругие и неупругие столкновения.
Рассмотрим столкновение двух шаров, скорости которых направлены вдоль линии, соеди-няющей их центры (центральный удар). Будем считать систему шаров замкнутой и полную энергию шаров до и после удара одинаковой. Такой удар называется абсолютно упругим. Запишем закон сохранения импульса в проекции на ось 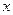 , проходящую через центры шаров, и закон сохранения энергии:
, проходящую через центры шаров, и закон сохранения энергии:
 ,
,
 .
.
Считая проекции скоростей 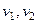 до удара заданными, из этой системы уравнений находим проекции скоростей шаров
до удара заданными, из этой системы уравнений находим проекции скоростей шаров 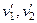 после удара
после удара
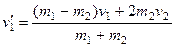 ,
,  .
.
Рассмотрим различные частные случаи.
1) Массы шаров одинаковы: 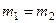 . В этом случае
. В этом случае  ,
,  , то есть шары обмениваются скоростями.
, то есть шары обмениваются скоростями.
2) Второй шар покоился до удара: 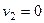 . Тогда
. Тогда 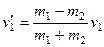 ,
,  . При
. При 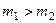 и
и  шары после удара движутся в одну сторону:
шары после удара движутся в одну сторону:  . При
. При 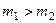 более легкий шар отражается в противоположном направлении, то есть
более легкий шар отражается в противоположном направлении, то есть 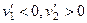 . При
. При 
 (отражение от неподвижной стенки).
(отражение от неподвижной стенки).
Перейдем к рассмотрению неупругих ударов. В этом случае часть кинетической энергии шаров переходит в тепловую энергию 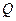 :
:
 .
.
Если величина 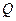 неизвестна, то решить задачу о столкновении в общем случае невоз-можно. Однако, есть один очень важный частный случай, когда задача решается до конца. Абсолютно неупругий удар – тела после удара движутся с одинаковой скоростью (“слипаются”).
неизвестна, то решить задачу о столкновении в общем случае невоз-можно. Однако, есть один очень важный частный случай, когда задача решается до конца. Абсолютно неупругий удар – тела после удара движутся с одинаковой скоростью (“слипаются”).
В этом случае закон сохранения импульса принимает вид:
 . Отсюда
. Отсюда  .
.
Из закона сохранения полной энергии с учетом количества тепла находим
 .
.
Удобно записать это выражение в следующем виде:
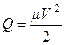 , где
, где 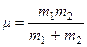 - приведенная масса ,
- приведенная масса , 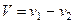 - относительная скорость
- относительная скорость
сталкивающихся тел.
Нецентральный удар
 Разложим скорости шаров в момент столкновения на нормальную и тангенциальную составляющие по отношению к плоскости касания шаров. В этом случае законы сохранения импульса и энергии для абсолютно упругого удара можно представить в следующем виде
Разложим скорости шаров в момент столкновения на нормальную и тангенциальную составляющие по отношению к плоскости касания шаров. В этом случае законы сохранения импульса и энергии для абсолютно упругого удара можно представить в следующем виде
 ,
,
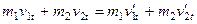 ,
,
 .
.
Итак, имеем три уравнения для четырех неизвестных. Поэтому задача не имеет однознач-ного решения. Такое решение существует в случае идеально гладких шаров (нет сил тре-ния), когда  . При этом одно уравнение исключается и остается две неизвестные величины.
. При этом одно уравнение исключается и остается две неизвестные величины.
Описание столкновений в системе центра масс
Центр масс двух сталкивающихся тел движется со скоростью
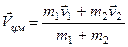 .
.
Если система тел является замкнутой, то 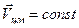 . Систему отсчета, в которой заданы скорости
. Систему отсчета, в которой заданы скорости 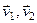 будем называть лабораторной системой отсчета. В ней мы рассматриваем процесс столкновения тел. Оказывается, что более удобно с вычислительной точки зрения изучать такой процесс в системе центра масс двух тел, движущейся со скоростью
будем называть лабораторной системой отсчета. В ней мы рассматриваем процесс столкновения тел. Оказывается, что более удобно с вычислительной точки зрения изучать такой процесс в системе центра масс двух тел, движущейся со скоростью 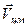 . Будем обозначать величины в системе центра масс индексом “0”. В силу того, что центр масс в такой системе неподвижен, для импульсов до и после столкновения имеют место соотношения
. Будем обозначать величины в системе центра масс индексом “0”. В силу того, что центр масс в такой системе неподвижен, для импульсов до и после столкновения имеют место соотношения
 ,
,  .
.
Тогда с помощью закона сохранения энергии
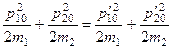
легко получить, что
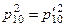 ,
, 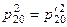 .
.
 Это означает, что в системе центра масс импульсы тел до столкновения и после столкновения противоположно направлены и имеют одинаковую абсолютную величину (см. рис. 2). В результате взаимодействия тел происходит поворот импульсов в системе центра масс на некоторый угол
Это означает, что в системе центра масс импульсы тел до столкновения и после столкновения противоположно направлены и имеют одинаковую абсолютную величину (см. рис. 2). В результате взаимодействия тел происходит поворот импульсов в системе центра масс на некоторый угол  . Значение этого угла можно найти только если известны силы взаимодействия между телами. Рассмотрим важный частный случай, когда второе тело в лабораторной системе покоится до столкновения
. Значение этого угла можно найти только если известны силы взаимодействия между телами. Рассмотрим важный частный случай, когда второе тело в лабораторной системе покоится до столкновения 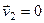 . Тогда
. Тогда
 ,
,  ,
,  ,
,  .
.

Эти соотношения приводят к удобному графическому приему, представленному на рис. 3. Пусть 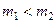 . Тогда
. Тогда  . Угол
. Угол 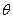 между вектором скорости налетающей частицы
между вектором скорости налетающей частицы 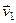 до столкновения и вектором скорости
до столкновения и вектором скорости  после столкновения называется углом рассеяния. Рассмотренный случай столкновения соответствует, в частности, опытам опытам Резерфорда по рассеянию
после столкновения называется углом рассеяния. Рассмотренный случай столкновения соответствует, в частности, опытам опытам Резерфорда по рассеянию  - частиц на тяжелых ядрах. Эти опыты привели в дальнейшем к созданию атомной физики. В случае, когда
- частиц на тяжелых ядрах. Эти опыты привели в дальнейшем к созданию атомной физики. В случае, когда  (налетающая частица тяжелее покоящеся),
(налетающая частица тяжелее покоящеся),  и точка
и точка 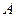 будет лежать вне окружности. При этом угол рассеяния будет ограничен некоторым значением
будет лежать вне окружности. При этом угол рассеяния будет ограничен некоторым значением  для которого отрезок
для которого отрезок 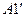 является касательной к окружности и
является касательной к окружности и 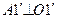 . Отсюда легко получить
. Отсюда легко получить
 .
.
Система центра масс обычно используется для расчета движения двух взаимодействующих тел (задача двух тел).
ЛЕКЦИЯ 7
Момент количества движения. Момент инерции твердого тела.
Мы рассмотрели два закона сохранения в механике: закон сохранения импульса и закон сохранения энергии. Каждый из законов сохранения в физике является следствием соответ-ствующего типа симметрии. Так закон сохранения импульса вытекает из однородности пространства, а закон сохранения энергии из однородности времени. Изотропность прост-ранства приводит к сохранению третьей важнейшей физической величины – момента импульса или момента количества движения.
Момент количества движения материальной точки 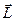

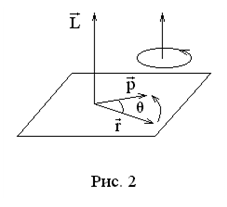
Модуль момента количества движения определяется как (см. рис. 1)
 .
.
Направление вектора 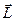 определяется по следующему правилу. Вектор
определяется по следующему правилу. Вектор 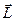 перпендику-лярен плоскости, в которой лежат вектора
перпендику-лярен плоскости, в которой лежат вектора 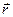 и
и 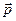 . При этом, если вращать вектор
. При этом, если вращать вектор 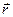 по напралению к вектору
по напралению к вектору 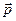 , то направление
, то направление 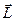 определяется движением правого винта при таком вращении (см. рис. 2).
определяется движением правого винта при таком вращении (см. рис. 2).
Такое действие над векторами 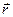 и
и 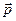 в векторной алгебре называется векторным произве-дением вектора
в векторной алгебре называется векторным произве-дением вектора 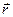 на вектор
на вектор 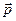 и обозначется следующим образом
и обозначется следующим образом
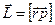 .
.
Отметим, что в соответствии с таким правилом в векторном произведении важен порядок сомножителей. При перестановке сомножителей меняется знак векторного произведения
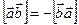 .
.
Для вектора момента импульса можно получить уравнение аналогичное уравнению второго закона Ньютона для импульса. Вычислим для этого производную по времени от 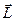 :
:
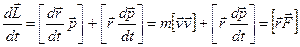 .
.
Слагаемое  равно нулю по определению векторного произведения. Последнее слага-емое в правой части называется моментом силы и обозначается
равно нулю по определению векторного произведения. Последнее слага-емое в правой части называется моментом силы и обозначается
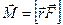 .
.
Таким образом уравнение, описывающее изменение момента импульса со временем имеет вид:
 .
.
Оно очень похоже на уравнение второго закона Ньютона: вместо импульса стоит момент импульса, а вместо силы – момент силы.
Для системы 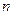 материальных точек
материальных точек
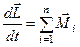 , где
, где  - полный момент импульса системы.
- полный момент импульса системы.
Замкнутая система 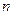 материальных точек
материальных точек
 Рассмотрим две точки с номерами
Рассмотрим две точки с номерами 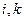 . По третьему закону Ньютона
. По третьему закону Ньютона  . Тогда
. Тогда
 ,
,
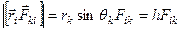 и
и  (см. рис. 3).
(см. рис. 3).
Величина 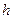 называется плечом силы относительно т. О. Отсюда следует, что
называется плечом силы относительно т. О. Отсюда следует, что  ,
, 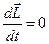 ,
, 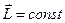 .
.
Таким образом имеет место следующий закон.
Закон сохранения момента количества движения
Полный момент количества движения замкнутой системы материальных точек остается постоянным.
Момент количества движения твердого тела, вращающегося вокруг фиксированной оси.
Мысленно разобьем твердое тело на малые элементы, которые можно считать материаль-ными точками. Момент количества движения i – го элемента
 .
.
 Направим ось
Направим ось 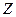 вдоль оси вращения и представим вектор
вдоль оси вращения и представим вектор 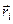 в виде суммы векторов
в виде суммы векторов 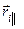 и
и 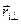 , направленных соответствен-но параллельно и перпендикулярно к оси вращения (см. рис. 4).
, направленных соответствен-но параллельно и перпендикулярно к оси вращения (см. рис. 4).
Тогда
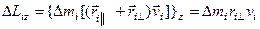 .
.
Так как каждый элемент вращается по окружности с угловой скоростью  , то
, то 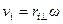 . Следовательно, проекция полного момента импульса на ось вращения
. Следовательно, проекция полного момента импульса на ось вращения
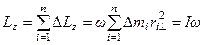 .
.
Величина  при
при  называется моментом инерции тела относительно заданной оси. Она описывает инерционные свойства вещества во вращательном движении тела. Через момент инерции выражается также кинетическая энергия вращательного движения:
называется моментом инерции тела относительно заданной оси. Она описывает инерционные свойства вещества во вращательном движении тела. Через момент инерции выражается также кинетическая энергия вращательного движения:
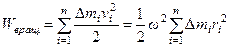 или
или 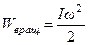 .
.
Вычисление момента инерции в общем случае сводится к вычислению объемного итеграла:
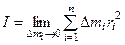 или
или  .
.
Производя соответствующее интегрирование можно найти моменты инерции тел различной формы относительно заданных осей. Приведем значения моментов инерции простейших однородных тел.
1) Полый тонкостенный цилиндр с массой 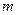 и радиусом
и радиусом  . Ось совпадает с осью симметрии.
. Ось совпадает с осью симметрии. 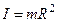
2) Сплошной цилиндр с той же осью.  .
.
3) Сплошной шар с той же осью 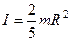 .
.
4) Тонкий стержень длины  . Ось перпедикулярна стержню и проходит через его конец.
. Ось перпедикулярна стержню и проходит через его конец. 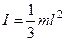 .
.
Теорема Штейнера
Пусть момент инерции тела массы 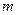 относительно оси, проходящей через центр масс равен
относительно оси, проходящей через центр масс равен  . Тогда его момент инерции относительно любой оси параллельной оси, проходящей через центр масс и отстоящей от нее на расстоянии
. Тогда его момент инерции относительно любой оси параллельной оси, проходящей через центр масс и отстоящей от нее на расстоянии 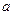 равен
равен
 .
.
ЛЕКЦИЯ 8
Основной закон вращательного движения твердого тела.
Снова мысленно разобьем тело на малые элементы 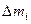 , которые можно считать материальными точками. Тогда для полного момента импульса
, которые можно считать материальными точками. Тогда для полного момента импульса  и полного момента сил
и полного момента сил  имеем (см. лекцию 7):
имеем (см. лекцию 7):
 . (1)
. (1)
Это уравнение называется основным законом вращательного движения в общем случае. При этом ось вращения может менять свое положение в пространстве и внутри тела.
Вращательное движение твердого тела вокруг фисированной оси

Рассмотрим очень важный частный случай вращения твердого под действием внешних сил вокруг фиксированной оси. Направим ось 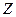 системы координат вдоль этой оси. Разложим радиус-вектор
системы координат вдоль этой оси. Разложим радиус-вектор 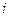 - го элемента
- го элемента 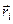 на вектры
на вектры 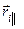 и
и 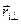 , параллельный и перпендикулярный к оси вращения. Аналогичное разложение проведем для силы
, параллельный и перпендикулярный к оси вращения. Аналогичное разложение проведем для силы  , действущей на
, действущей на 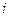 - й элемент. Тогда момент импульса этого элемента можно представить в виде
- й элемент. Тогда момент импульса этого элемента можно представить в виде
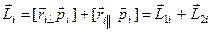 ,
,
где 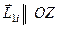 ,
, 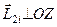 .
.
Для осесимметричного тела 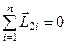 и при вычислении полного момента импульса останется только проекция на ось вращения:
и при вычислении полного момента импульса останется только проекция на ось вращения:
 .
.
Проекция на ось  момента силы, действущей на
момента силы, действущей на  - й элемент , очевидно, выражается только через
- й элемент , очевидно, выражается только через  и
и 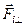 :
:
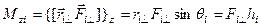 ,
,
где  - угол между векторами
- угол между векторами  ,
,  - плечо силы
- плечо силы 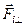 относительно оси.
относительно оси.
Проекция полного момента силы на ось 
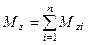 .
.
В проекции на ось  уравнение (1) имеет вид:
уравнение (1) имеет вид:
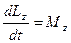 , где
, где 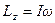 . Его можно переписать через угловое ускорение
. Его можно переписать через угловое ускорение 
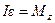
Это основной закон вращательного движения для случая фиксированной оси.
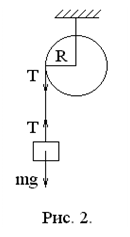 Пример. Рассмотрим следующую задачу. Сплошной цилиндр радиуса
Пример. Рассмотрим следующую задачу. Сплошной цилиндр радиуса  и массы
и массы 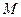 может вращаться вокруг оси, совпадающей с его осью симметрии. На цилиндр намотана невесомая нерастяжимая нить, к концу которой прикреплено тело массы
может вращаться вокруг оси, совпадающей с его осью симметрии. На цилиндр намотана невесомая нерастяжимая нить, к концу которой прикреплено тело массы 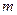 . Нужно найти ускорение этого тела.
. Нужно найти ускорение этого тела.
Для решения этой задачи запишем 2 – й закон Ньютона для тела 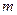 в проекции на направление его движения и основной закон вращатель-ного движения для цилиндра:
в проекции на направление его движения и основной закон вращатель-ного движения для цилиндра:
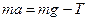 ,
, 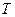 - сила натяжения нити,
- сила натяжения нити,
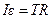 .
.
Кроме этого используем связь между 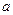 и
и  :
: 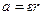 (лекция 2).
(лекция 2).
Решая эту систему уравнений и подставляя  , находим
, находим  .
.
Суммарный момент сил, действующих на тело в поле тяжести
 На элемент
На элемент  действует момент силы тяжести
действует момент силы тяжести
(ось  направлена на нас)
направлена на нас)
 .
.
Тогда проекция полного момента силы тяжести
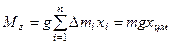 ,
, 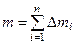 - полная масса
- полная масса
тела,  - координата
- координата 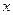 центра масс
центра масс
тела. Значит при вычислении момента сил тяжести можно считать, что сила 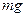 приложена к центру масс тела.
приложена к центру масс тела.
ЛЕКЦИЯ 9
Общий случай вращательного движения твердого тела. Гироскопические явления.
 Рассмотрим движение плоского твердого тела в его собственной плоскости
Рассмотрим движение плоского твердого тела в его собственной плоскости 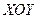 . Выберем в нем две произвольные точки
. Выберем в нем две произвольные точки 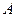 и
и  . Так как тело является твердым, то при его движении
. Так как тело является твердым, то при его движении
 .
.
Продифференцируем это соотношение по времени
 .
.
Пусть в данный момент времени 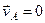 . Тогда для всех точек
. Тогда для всех точек  имеем
имеем  . Это означает, что скорости перпендикулярны соответствующим радиусам. Следовательно, можно говорить о вращении в данный момент времени вокруг оси, проходящей через точку
. Это означает, что скорости перпендикулярны соответствующим радиусам. Следовательно, можно говорить о вращении в данный момент времени вокруг оси, проходящей через точку 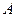 .
.
Мгновенная ось вращения - прямая, проходящая через точки тела, скорости которых в данный момент времени равны нулю.
Например, для цилиндра, катящегося по плоскости, мгновенная ось вращения проходит через точки соприкосновения цилиндра с плоскостью (лекция 2).
Имеет место важная теорема, относящаяся к движению тела с одной неподвижной точкой. Мы приведем ее без доказательства.
Теорема Эйлера
Твердое тело, имеющее одну неподвижную точку, может быть переведено из произвольного положения в другое произвольное положение путем поворота вокруг некоторой оси, прохо-дящей через эту точку.
Произвольное движение твердого тела.
Его можно представить как совокупность поступательного движения всего тела со ско-ростью  его некоторой точки
его некоторой точки  (основная точка) и вращательного с угловой скоростью
(основная точка) и вращательного с угловой скоростью  вокруг мгновенной оси, проходящей через эту точку. При этом угловая скорость
вокруг мгновенной оси, проходящей через эту точку. При этом угловая скорость  не зависит от выбора основной точки
не зависит от выбора основной точки  .
.
Выберем в качестве основной точки центр масс тела. Пусть 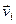 - скорость вращательного движения
- скорость вращательного движения  - го элемента тела относительно мгновенной оси. Тогда полную кинетическую энергию тела можно представить в виде
- го элемента тела относительно мгновенной оси. Тогда полную кинетическую энергию тела можно представить в виде
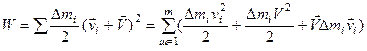 .
.
Последнее слагаемое в правой части равенства равно при суммировании дает нуль, так как ось проходит через центр масс. Тогда приходим к выражению (теорема Кёнига)
 .
.
Получим одно важное соотношение между энергией вращательного движения 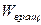 и моментом импульса тела
и моментом импульса тела  . Оно понадобится нам в дальнейшем. Можно легко убедиться в том, что скорость вращения
. Оно понадобится нам в дальнейшем. Можно легко убедиться в том, что скорость вращения 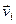 и угловая скорость
и угловая скорость  связаны соотношением
связаны соотношением  . Тогда
. Тогда
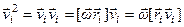 .
.
Последнее из равенств доказывается в векторной алгебре. В этом случае для 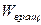 получим
получим
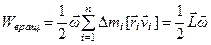 .
.
В частном случае вращения осесимметричного тела вокруг его оси 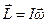 и
и 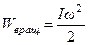 .
.
Гироскоп – быстровращающееся осесимметричное тело, ось вращения которого может изменять свое направление в пространстве.
Движение гироскопа описывается основным законом вращательного движения вобщем виде
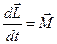 .
.
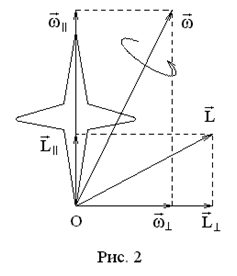 При этом ось вращения и момент импульса не обяза-тельно совпадают с осью гироскопа. Рассмотрим движение гироскопа с одной неподвижной точкой (т. О на рис. 2). Тогда по теореме Эйлера в каждый момент времени происходит вращение вокруг мгновенной оси проходящей через т. О. Разложим вектора
При этом ось вращения и момент импульса не обяза-тельно совпадают с осью гироскопа. Рассмотрим движение гироскопа с одной неподвижной точкой (т. О на рис. 2). Тогда по теореме Эйлера в каждый момент времени происходит вращение вокруг мгновенной оси проходящей через т. О. Разложим вектора  на составляющие вдоль оси гироскопа и перпендикуляр-ные к оси гироскопа (см. рис. 2). Физический смысл суммы векторов
на составляющие вдоль оси гироскопа и перпендикуляр-ные к оси гироскопа (см. рис. 2). Физический смысл суммы векторов  состоит в том, что при этом тело вращается вокруг собственной оси с угловой скоростью
состоит в том, что при этом тело вращается вокруг собственной оси с угловой скоростью 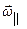 , а сама эта ось вращается вокруг оси перпендикулярной к собсвенной со скоростью
, а сама эта ось вращается вокруг оси перпендикулярной к собсвенной со скоростью  .
.
Момент импульса гироскопа можно представить в виде
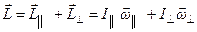 ,
,
где  - моменты инерции гироскопа относительно соответствующих осей. Тогда
- моменты инерции гироскопа относительно соответствующих осей. Тогда
 .
.
Свободный гироскоп (  ).
).
В этом случае выполняются законы сохранения момента импульса и энергии
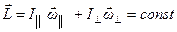 ,
,
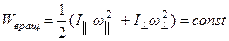 .
.
Из этих уравнений следует, что при движении свободного гироскопа значения 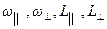 остаются постоянными. Это означает, что имеет место так называемая свободная регулярная прецессия: в каждый момент времени движение свободного гиро-скопа есть вращение вокруг мгновенной оси, проходящей неподвижную точку опоры; направление вектора
остаются постоянными. Это означает, что имеет место так называемая свободная регулярная прецессия: в каждый момент времени движение свободного гиро-скопа есть вращение вокруг мгновенной оси, проходящей неподвижную точку опоры; направление вектора  неизменно в пространстве, а ось гироскопа и мгновенная ось вращения вращаются вокруг
неизменно в пространстве, а ось гироскопа и мгновенная ось вращения вращаются вокруг  с постоянной угловой скоростью
с постоянной угловой скоростью  .
.
Вынужденная прецессия гироскопа
При кратковременном воздействии на гироскоп 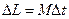 мало по сравнению с
мало по сравнению с  в силу большой угловой скорости вращения вокруг собственной оси. То есть имеет место устойчи-вость движения свободного гироскопа. Это находит применение в многочисленных приложениях (автопилоты, гирокомпасы, движение мотоциклов и велосипедов и т. д.).
в силу большой угловой скорости вращения вокруг собственной оси. То есть имеет место устойчи-вость движения свободного гироскопа. Это находит применение в многочисленных приложениях (автопилоты, гирокомпасы, движение мотоциклов и велосипедов и т. д.).
Совсем по-другому ведет себя несвободный гироскоп, находящийся под действием постоян-ной силы.
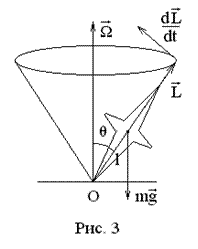
Рассмотрим движение гироскопа с одной неподвижной точкой в поле тяжести.
Будем считать, что 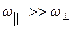 (приближенная теория гироскопа). В этом случае момент импульса гироскопа направлен вдоль его оси и равен
(приближенная теория гироскопа). В этом случае момент импульса гироскопа направлен вдоль его оси и равен 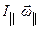 . Основной закон вращательного движения имеет вид:
. Основной закон вращательного движения имеет вид:
 . С другой стороны можно считать, что
. С другой стороны можно считать, что 
является “скоростью движения” конца вектора  . Тогда по аналогии с формулой
. Тогда по аналогии с формулой 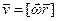 можно записать, что
можно записать, что
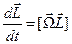 . Отсюда
. Отсюда 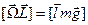 или
или  . Отсюда находим
. Отсюда находим
 .
.
Ось гироскопа в этом случае описывает конус, совершая вращение с угловой скоростью 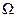 .
.
Такое движение называется вынужденной прецессией гироскопа под действием внешней силы. Гироскопические явления играют важную роль в самых разнообразных физических системах, от механических до атомных.
ЛЕКЦИЯ 10
Дата добавления: 2016-01-09; просмотров: 1337;
