Криволинейное движение. Кинематика твердого тела.
Основные понятия кинематики.
Кинематика – раздел механики, в котором описывается движение без рассмотрения его причин.
Материальная точка - тело, размерами которого можно пренебречь при изучении его движения. Например, Землю можно считать материальной точкой при ее движении вокруг Солнца.
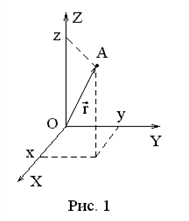 Система отсчета – тело, или система тел, относи-тельно которого определяется положение рассматриваемого движущегося тела. Для задания положения материальной точки используются системы координат. Декартова система координат – три взаимно перпендикулярные направленные оси. Будем использовать правую систему координат: при повороте правого винта по направлению от оси
Система отсчета – тело, или система тел, относи-тельно которого определяется положение рассматриваемого движущегося тела. Для задания положения материальной точки используются системы координат. Декартова система координат – три взаимно перпендикулярные направленные оси. Будем использовать правую систему координат: при повороте правого винта по направлению от оси 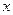 к оси
к оси 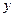 он должен двигаться вдоль оси
он должен двигаться вдоль оси 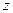 . Существуют и другие системы координат. Так, при описании движения мате-риальной точки в грвитационном поле мы в дальнешем будем пользоваться так называемой полярной системой координат.
. Существуют и другие системы координат. Так, при описании движения мате-риальной точки в грвитационном поле мы в дальнешем будем пользоваться так называемой полярной системой координат.
Радиус-вектор 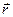 данной точки
данной точки 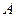 - отрезок прямой, проведенный из начала координат
- отрезок прямой, проведенный из начала координат 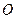 в т.
в т. 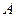 , направленный из т.
, направленный из т. 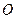 в т.
в т. 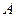 (рис. 1). При этом проекции радиуса-вектора на оси
(рис. 1). При этом проекции радиуса-вектора на оси 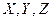 являются декартовыми координатами
являются декартовыми координатами 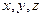 т.
т. 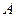 .
.
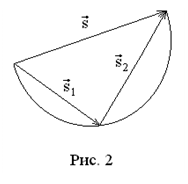 Вектор перемещения
Вектор перемещения 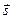 - вектор, соединяющий начальную точку траектории материальной точки с конечной и направленный из начальной точки в конечную. Из самого определения вектора перемещения следует правило сложения перемещений: если материальная точка совершила два последовательных перемещения
- вектор, соединяющий начальную точку траектории материальной точки с конечной и направленный из начальной точки в конечную. Из самого определения вектора перемещения следует правило сложения перемещений: если материальная точка совершила два последовательных перемещения 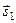 и
и 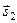 , то полное перемещение равно векторной сумме
, то полное перемещение равно векторной сумме 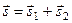 (рис. 2).
(рис. 2).
Свойства векторных физических векторных величин, связанных с определенным направлением в пространстве, определяют правила выполнения действий над векторами. Значение вектора 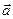 задется значениями его проекций на координатные оси
задется значениями его проекций на координатные оси 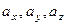 . Примем следующую форму записи векторных величин
. Примем следующую форму записи векторных величин 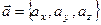 . В таких обозначениях правила действия над векторами сводятся к действиям над их проекциями.
. В таких обозначениях правила действия над векторами сводятся к действиям над их проекциями.
1. Сумма векторов.
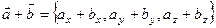 , где
, где 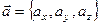 ,
, 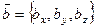 .
.
Это правило эквивалентно известному правилу параллелограмма.
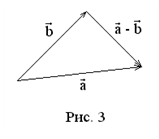
2. Разность векторов.
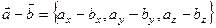 .
.
Это правило будем называть правилом треугольника (рис. 3).
Длина вектора определяется выражением
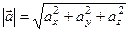 .
.
3. Умножение вектора на число.
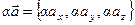 .
.
При 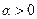 вектора
вектора 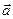 и
и 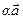 имеют одинаковое направление, а при
имеют одинаковое направление, а при 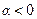 - противоположное.
- противоположное.
Прямолинейное движение материальной точки – движение вдоль прямой линии. Направим ось 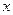 вдоль этой прямой. Пусть
вдоль этой прямой. Пусть 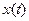 и
и 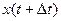 - значения координаты в два момента времени. Тогда
- значения координаты в два момента времени. Тогда 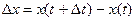 равно изменению
равно изменению 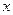 за промежуток времени
за промежуток времени 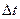 .
.
Скорость прямолинейного движения в момент времени 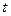 :
:
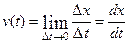 (производная
(производная 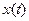 по времени).
по времени).
Ускорение прямолинейного движения:
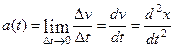 (производная
(производная 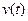 по времени, или вторая производная
по времени, или вторая производная 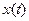 по времени).
по времени).
Равноускоренное движение – движение с постоянным ускорением ( 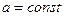 ).
).
В этом случае 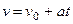 ,
, 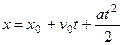 . Здесь
. Здесь 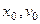 - значения координаты и скорости в начальный момент времени (начальные условия).
- значения координаты и скорости в начальный момент времени (начальные условия).
 Относительность движения и формула сложения скоростей.
Относительность движения и формула сложения скоростей.
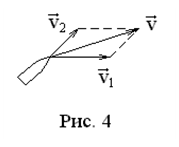
Пример. Лодка, плывущая по реке.
Пусть 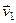 - скорость течения воды,
- скорость течения воды, 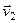 - скорость лодки относительно воды,
- скорость лодки относительно воды, 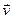 - скорость лодки относительно берега. Тогда из сложения перемещений
- скорость лодки относительно берега. Тогда из сложения перемещений 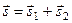 вытекает формула сложения скоростей
вытекает формула сложения скоростей 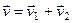 .
.
ЛЕКЦИЯ 2
Криволинейное движение. Кинематика твердого тела.
Дата добавления: 2016-01-09; просмотров: 805;
