Погрешности косвенных измерений

Искомое значение величины Y при косвенных измерениях находят путем согласованных измерений других величин Xi, связанных с измеряемой величи­ной известной зависимостью.

Величина Хi называется аргументом. Значения аргументов чаще всего определяют в результате прямых измерений.

Различают линейные и нелинейные косвенные измерения.

Для линейных косвенных измерений:

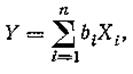
где bi — постоянный коэффициент; n — число слагаемых.

Для нелинейных косвенных измерений:

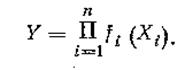
Оценка Y при линейных косвенных измерениях определяется по формуле:

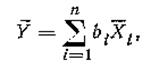
где Хi — оценка математического ожидания i-ro аргумента.

Погрешность косвенного измерения Y в данном случае:

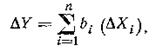
где ΔXi — погрешность измерения i-го аргумента.

Дисперсия оценки величины Y при косвенном линейном измерении:

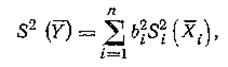
где 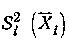—дисперсия оценки аргумента Xi

Это выражение верно в случае независимости погрешностей измерений аргументов.

При нелинейных косвенных измерениях значение Y оценивается выраже­нием:

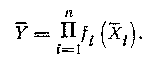
Такая оценка является несмещенной и состоятельной, если оценки Хi яв­ляются состоятельными.

Погрешность косвенного измерения в данном случае:

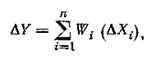
где Wi — коэффициент влияния 1-го аргумента:

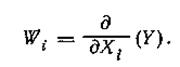
При отсутствии корреляционной зависимости между погрешностями изме­рений аргументов дисперсия оценки Y вычисляется по формуле:

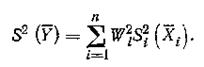
Если 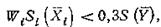то погрешность оценки 1-го аргумента несущественно влияет на погрешность косвенного измерения.

Аналогичный вывод можно сделать относительно нескольких (l) аргументов, если:

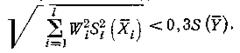
Повышение точности косвенного измерения необходимо обеспечивать за счет повышения точности оценки тех аргументов, которые дают существенный вклад в дисперсию оценки А.