Числовая оценка случайных погрешностей
Совокупность всех возможных значений исследуемой случайной погрешности называется генеральной совокупностью.
Множество значений случайной погрешности, полученное в результате наблюдения над нею, называют случайной выборкой или просто выборкой.
Число объектов в генеральной совокупности и в выборке характеризует их объем. Генеральная совокупность может иметь бесконечный объем.
Основной задачей является получение научно обоснованных выводов о числовых характеристиках генеральной совокупности случайных погрешностей по выборке.
Выборочная оценка должна обладать следующими свойствами:
· несмещенностью;
· эффективностью;
· состоятельностью.
Оценку А параметра А называют несмещенной, если ее математическое ожидание равно оцениваемому параметру.
Требование несмещенности гарантирует отсутствие систематических ошибок при оценке параметров.
Так как А — случайная величина, значение которой изменяется от выборки к выборке, то меру ее рассеивания характеризуют дисперсией D(A). Из двух оценок А следует отдать предпочтение той, которая обладает меньшим рассеиванием (т. е. меньшей дисперсией).
Несмещенную оценку А которая имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра А, вычисленных по выборкам одного и того же объема, называют эффективной оценкой.
Оценку А параметра А называют состоятельной, если при неограниченном увеличении объема выборки ее значение приближается сколь угодно близко к значению оцениваемого параметра.
На практике не всегда удается удовлетворить одновременно требованиям несмещенности, эффективности и состоятельности оценки параметра.
Иногда для простоты расчетов целесообразно использовать незначительно смещенную оценку.
Оценку неизвестного параметра генеральной совокупности одним числом называют точечной оценкой.
Точечной оценкой математического ожидания М(Х) случайной величины X является среднее арифметическое значение X, вычисленное по результатам m независимых наблюдений:
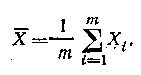
Эта оценка является несмещенной, состоятельной и эффективной. Она имеет дисперсию σ2/m, если дисперсия случайной величины X равна σ2.
Несмещенной оценкой дисперсии генеральной совокупности D(X) является исправленная выборочная дисперсия:
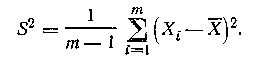
Эта оценка является состоятельной, но не эффективной.
При малом числе наблюдений необходимо использовать интервальное оценивание, так как в этом случае точечная оценка недостаточно надежна.
Необходимо по данным выборки построить числовой интервал, в котором с заранее выбранной вероятностью находится значение оцениваемого параметра.
Доверительным интервалом (А2—А1) для параметра А называют такой интервал, для которого с заранее выбранной вероятностью Р=1 — α, близкой к единице, можно утверждать, что:
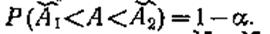
Чем меньше для выбранной вероятности (А2—А1), тем точнее оценка параметра А.
Доверительный интервал меняется от выборки к выборке.
Вероятность Р=1 — α называется доверительной вероятностью, а число α — уровнем значимости.
Выбор доверительной вероятности зависит от конкретной решаемой задачи.
Если случайная величина распределена нормально, а дисперсия этого распределения неизвестна, то доверительный интервал для математического ожидания М(Х) определяется неравенством:
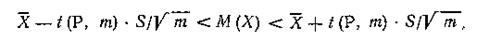
где t(P, m) —критерий Стьюдента, выбираемый их соответствующей таблицы, при доверительной вероятности Р и числе степеней свободы f = m—l.
Если случайная величина распределена нормально, доверительный интервал для дисперсии генеральной совокупности при доверительной вероятности Р=1 — α определяется неравенством:
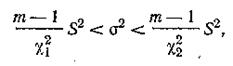
где χ2 — критерий Пирсона, выбираемый из соответствующей таблицы, который соответствует доверительной вероятности, равной 0,5α, для  ; определяется при
; определяется при 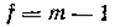 .
.
Дата добавления: 2016-01-09; просмотров: 757;
