Обнаружение грубых погрешностей

Если в полученной группе результатов измерений одно-два резко отлича­ются от остальных, а описки, ошибки в снятии показаний и тому подобные промахи не установлены, следует проверить, не являются ли они грубыми по­грешностями, подлежащими исключению.

При решении данной задачи пред­полагается, что результаты наблюдений подчиняются нормальному закону рас­пределения.

Грубые погрешности возникают при случайном резком изменении условий измерения.

Для решения задачи имеющиеся результаты измерения располагают в ва­риационный ряд монотонно возрастающих значений Xi (i=l, 2, ..., m).

Провер­ке подлежит наименьший Хi (или наибольший Хm) член ряда. Сначала вычис­ляются числовые характеристики результатов наблюдений:

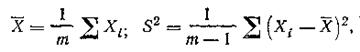
затем наблюдаемое значение критерия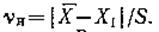

Задавшись доверительной вероятностью Р определяем по таблице критическое значение критерия νк, которое зависит также от числа измерений m.

Если vn<vк, то принимается гипотеза Hi—все наблюдения проводились в одинаковых условиях и значение Хi (или Хm) составляет с остальными резуль­татами однородную выборку.

Если это неравенство нарушается, т. е. vn>vк, то «подозрительный» результат Xi следует исключить из дальнейшего рассмо­трения.

Если в выборке несколько «подозрительных» результатов измерения, то данная процедура может применяться поочередно к каждому из них в отдель­ности.

Пример.

Результаты измерения выборки деталей, обработанных на бесцентровошлифовальном станке, образуют следующий ряд отклонений от но­минала (мкм): 26; 30; 25; 28; 40; 32; 26; 22; 28; 31. Требуется определить с доверительной вероятностью, равной 0,95 является ли отклонение в 40 мкм грубой погрешностью.

Решение,

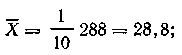
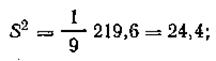
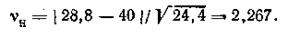
Согласно таблице, ν_К=2,294.

Так как ν_Н <ν_К, то отклонение в 40 мкм не является грубой ошибкой.

.