Фундаментальные положения

При передаче цифровой информации по каналу связи передают последовательность чисел в двоичном коде, т.е. последовательность нулей 0 и единиц 1. Прием информации состоит в том, чтобы с максимальной вероятностью отличить 0 от 1. При передаче информации (модулирующего сигнала) по радиоканалу используют различные методы модуляции (манипуляции –Keying), в основе которых в большинстве случаев лежит линейная модуляция с двойной боковой полосой(ДБП) [10].

Напомним, что при ДБП модулирующий сигнал a(t) переносят из области основных частот (baseband signal) на несущую радиочастоту f₀, так что радиосигнал ДБП

(4.1)

В спектральном представлении получим перенос спектра модулирующего сигнала, расположенного в полосе частот (F₁…F₂), на частоту f₀ в соответствии с рис. 4.1.

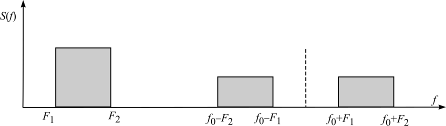
Рис. 4.1. Перенос спектра

В результате получаем 2 боковые полосы (f₀ + F₁)¼(f₀ + F₂) и (f₀− F₁)¼(f₀ − F₂) с подавленной несущей f₀.

Суть модуляции состоит в умножении модулирующего сигнала a(t) на несущую частоту U₀cosw₀t. Эту операцию выполняют в балансных модуляторах (смесителях) с последующей фильтрацией комбинационных частот высших порядков. Полоса радиосигнала П_рад в 2 раза больше полосы модулирующего сигнала П_мод.

Логические 0 и 1 можно передавать самыми разными способами. В модуляторе их обычно представляют биполярными сигналами одинаковой формы. Классическим представлением является передача 0 и 1 прямоугольными импульсами разной полярности: передаче 1 соответствует −А, а 0 +А (рис. 4.2). Длительность бита равна Т_В, а скорость передачи В = f_T = 1/T_B (бит/с).

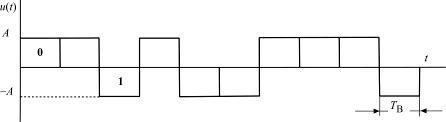
Рис. 4.2. Цифровой сигнал

Так как чередование 0 и 1 случайно, то спектры отдельных временных интервалов сигнала будут также случайными. При этом спектральные характеристики модулирующих сигналов тоже случайны.

Обобщенной спектральной характеристикой цифрового сигнала является энергетический спектр G(f), т.е. усредненная мощность, приходящаяся на полосу в 1 герц: G(f) (Вт/Гц).

Теорема 1. Если на временном интервале передачи цифрового сигнала появление 0 и 1 равновероятно (вероятность того и другого равна 0,5), а сами 0 и 1 передают в виде импульсов одинаковой формы, но разной полярности, то энергетический спектр G(f) и спектр одного импульса S(f) связаны между собой соотношением

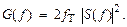(4.2)

Доказательство теоремы 1 можно найти в [13].

Определим энергетический спектр для важного в теоретическом плане цифрового сигнала с разнополярными прямоугольными импульсами для передачи 0 и 1 (рис. 4.2). Отдельный бит (импульс) такого сигнала представим симметричным на оси времени (рис. 4.3).

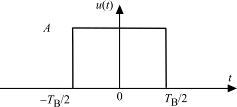
Рис. 4.3. Прямоугольный импульс

Его спектр (рис. 4.4):

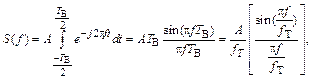
тогда

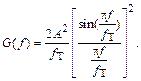(4.3)

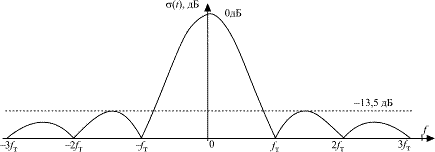
Рис. 4.4. Спектральная характеристика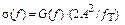
последовательности прямоугольных импульсов

Распространение спектра в область отрицательных частот соответствует понятию аналитического сигнала. Важно отметить, что спектр бесконечен (что и следовало ожидать для импульсов конечной длительности) и обращается в 0 на частоте f_T и кратных ей kf_T.

Радиосигнал всегда имеет жестко ограниченную полосу частот, поэтомуо спектры радиосигналов приходится ограничивать. Но конечному по ширине спектру соответствует бесконечный по длительности сигнал. Следовательно, импульсы, передающие соседние биты, будут накладываться друг на друга, что называют межсимвольной интерференцией. Наличие межсимвольной интерференции увеличивает вероятность ошибок при приеме.

Возникает проблема: можно ли при ограничении спектра сигнала обеспечить его прием без межсимвольной интерференции? На этот вопрос дает ответ следующая теорема.

Теорема 2. Может быть обеспечен прием сигнала без межсимвольной интерференции, если спектральная характеристика одного импульса представляет собой прямоугольник, ограниченный полосой −f_T/2…+f_T/2 (рис. 4.5), называемой полосой Найквиста П_N.

Рис. 4.5. Прямоугольная спектральная характеристика

В соответствии с обратным преобразованием Фурье

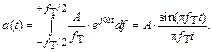(4.4.)

Сигнальный импульс a(t) показан на рис. 4.6.

Рис. 4.6. Сигнальный импульс

В тактовые моменты времени t = kT_B, кроме t = 0, сигнал обращается в нуль, поэтому, если в приемнике при наличии тактовой синхронизации снимать значения сигнала в тактовые моменты времени, прием будет происходить без межсимвольной интерференции (рис. 4.7).

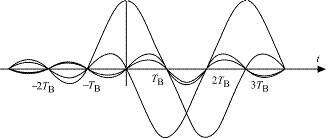
Рис. 4.7. Последовательность сигнальных импульсов

Разумеется, на практике все оказывается сложнее, так как на передаваемый сигнал накладываются помехи, но теорема 2 показывает возможность передачи цифрового сигнала в ограниченной полосе со значительным устранением влияния межсимвольной интерференции.

Остановимся на том, как сформировать сигнал с требуемыми спектральными характеристиками. Сигнал (рис. 4.6) со спектром, близким к идеальному (рис. 4.5), может быть сформирован методом прямого цифрового синтеза. Однако можно смягчить требования к спектру сигнала, сделав плавные спады вблизи частот –f_T/2 и f_T/2. Отсутствие межсимвольной интерференции в тактовые моменты времени обеспечивает равенство площадей заштрихованных площадок на характеристике энергетического спектра (рис. 4.8) [14]. Ширина спектра при этом увеличивается в (1+α) раз. На практике коэффициент скругления α = 0,25…0,4.

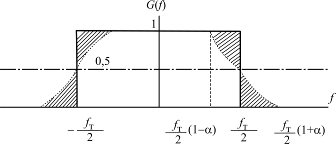
Рис. 4.8. Оптимальный энергетический спектр цифровых сигналов

Для реализации спектральной характеристики такого вида часто применяют фильтры с характеристиками типа приподнятого косинуса.

В области положительных частот такой фильтр можно описать следующими параметрами:

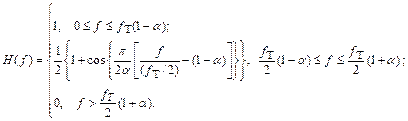(4.5)

Важнейшей задачей при выборе метода модуляции является эффективное использование частотного ресурса. Предварительно кратко напомним классификацию сигналов.

По объему алфавита цифрового сообщения М радиосигналы делят на двоичные (М = 2) и многопозиционные (М > 2).

По методу формирования можно разделять сигналы объемно-сферической (ОСУ) и поверхностно-сферической укладки (ПСУ).

К сигналам ОСУ относятся разновидности сигналов амплитудной, амплитудно-фазовой, амплитудно-частотно-фазовой модуляции и др. Для приема этих сигналов необходимо поддерживать постоянный уровень сигналов на входе демодулятора, что представляет определенные сложности, кроме этого, передатчик сигналов ОСУ должен работать в линейном режиме, что, в свою очередь, проблематично для мобильных станций.

Для сигналов поверхностно-сферической укладки поиск наилучших ансамблей сигналов осуществляется путем нахождения сигнальных точек в узлах пространственной решетки, имеющей регулярную структуру.

При так называемой плотнейшей поверхностно-сферической укладке сигнальные точки располагаются равномерно на окружности с минимальным углом между соседними векторами

(4.6)

и минимальным расстоянием между сигнальными точками

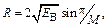(4.7)

где E_В – энергия информационного бита.

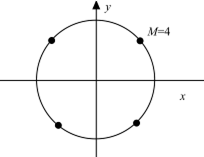
Рис. 4.9. Пример созвездия сигнала ПСУ