Эффективность цифровых систем передачи
Спектральная (частотная) эффективность цифровой системы опре-деляется как отношение скорости передачи информации B, бит/с, к полной полосе частот канала ПW, Гц,
|
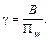 (4.8)
(4.8)
Спектральная эффективность измеряется числом битов в секунду, приходящихся на 1 Гц полосы канала, т.е. бит/(с·Гц).
Свяжем коэффициент спектральной эффективности с полосой Найквиста ПN и коэффициентом скругления спектра α, значение которого характеризует расширение практически занимаемой спектром сигнала полосы частот канала ПL сверх полосы Найквиста ПN (рис. 4.7):
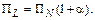 (4.9)
(4.9)
Тогда реальную спектральную эффективность определяет выражение
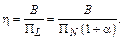 (4.10)
(4.10)
В идеальном случае при полном использовании всей полосы частот канала, когда ПW = ПL, показатели эффективности η и γ совпадают, т.е. γ = η.
Критерий потенциальной спектральной эффективности конкретного метода модуляции γ0 соответствует коэффициенту η или γ при ПW = В и α = 0.
|
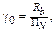 (4.11)
(4.11)
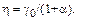 (4.12)
(4.12)
При использовании многопозиционной цифровой манипуляции
 (4.13)
(4.13)
где М – число элементов пространства сигналов; BS – скорость передачи символов цифрового потока.
Согласно критерию Найквиста максимальная скорость передачи символов в выделенной полосе частот численно равна
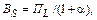 (4.14)
(4.14)
так что
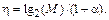
Вывод 1. Для повышения спектральной эффективности η необходимо увеличивать кратность модуляции lg2(M), что достигается применением многопозиционных методов модуляции (манипуляции), и снижать значение коэффициента скругления α, тем самым увеличивая крутизну среза спектра модулирующего сигнала.
Энергетическую эффективность определяют показателем β:
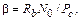 (4.15)
(4.15)
где РС – средняя мощность модулированного сигнала; N0 = kT – односторонняя спектральная плотность мощности аддитивного белого гауссовского шума (АБГШ) на входе приемника.
|
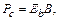 (4.16)
(4.16)
где Еb – энергия сигнала на бит информации на входе приемного фильтра, получаем
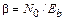 . (4.17)
. (4.17)
Вывод 2. Коэффициент β – величина, обратная отношению энергии на бит в передаваемом сигнале к плотности шума на входе приемника.
При согласованной найквистовской фильтрации шумовая полоса приемника совпадает с полосой Найквиста, тогда мощность шума на входе решающего устройства
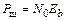 . (4.18)
. (4.18)
Обозначив отношение сигнал/шум
|

из (4.15) получаем
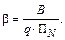 (4.19)
(4.19)
Далее, подставив в (4.20) отношение B/ПN = γ0 = η(1+α), получаем
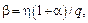 (4.20)
(4.20)
или
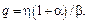 (4.21)
(4.21)
Вывод 3. Коэффициенты η и β взаимосвязаны.
Как известно, пропускная способность (максимально возможная скорость передачи информации) частотно-ограниченного канала с аддитивным белым гауссовским шумом определяется формулой Шеннона [12]:
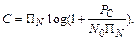 (4.22)
(4.22)
При выполнении условий теоремы максимум B = С и тогда
|
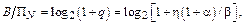
откуда вытекает следующее соотношение для верхней границы эффективности передачи информации:
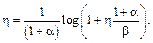 (4.23)
(4.23)
Из (4.23) получаем формулу для энергетической эффективности β как функции реальной спектральной эффективности η и коэффициента скругления спектра α:
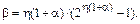 (4.24)
(4.24)
Для оценки спектральной эффективности удобно также использовать показатель компактности спектра γ:
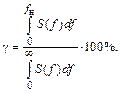 (4.25)
(4.25)
Фазовая модуляция
В настоящее время методы цифровой модуляции в мобильной связи вытеснили своих аналоговых предшественников.
При передаче цифровой информации по каналам связи главной задачей модулятора является отображение цифровой информации, а именно: последовательности двоичных символов, посредством изменения значений параметров физических переносчиков информации.
Поскольку такое изменение, как правило, оказывается дискретным, то термин «модуляция» часто заменяют термином «манипуляция». Если для передачи информации имеется М возможных значений физических параметров, то указанное отображение осуществляется посредством выбора набора из  двоичных символов и его сопоставления одной из
двоичных символов и его сопоставления одной из  форм, каждая из которых определяется конкретными значениями параметров сигналов, имеющих определенную энергию.
форм, каждая из которых определяется конкретными значениями параметров сигналов, имеющих определенную энергию.
Дата добавления: 2016-01-07; просмотров: 2549;
