Взаиморасположение прямых

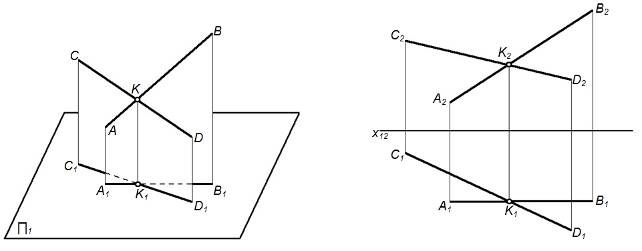
Две прямые в пространстве могут быть пересекающимися, параллельными и скрещивающимися. На рисунке 10а дано наглядное изображение прямых АВ и СD, пересекающихся в точке К, а также их комплексный чертеж (рисунок 10б).

а) б)

Рисунок 10 – Пересекающиеся прямые

Признаком пересекающихся прямых на комплексном чертеже является то, что их одноименные проекции пересекаются между собой, а проекции точек пересечения лежат на одной линии связи.

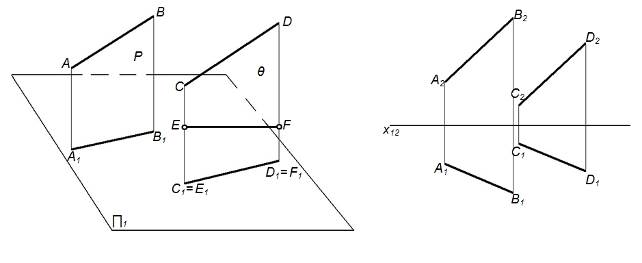
На рисунке 11а дано наглядное изображение параллельных прямых АВ и СD, а также их комплексный чертеж (рисунок 11б). Если в пространстве прямые параллельны, то их одноименные проекции тоже параллельны. Действительно, проецирующие плоскости Р и q, проведены через параллельные прямые АВ и СD (рисунок 11). С плоскостью проекций П1 они пересекаются по параллельным прямым А1В1 и С1D1 – проекциям прямых АВ и СD на плоскости П1.

а) б)

Рисунок 11 – Параллельные прямые

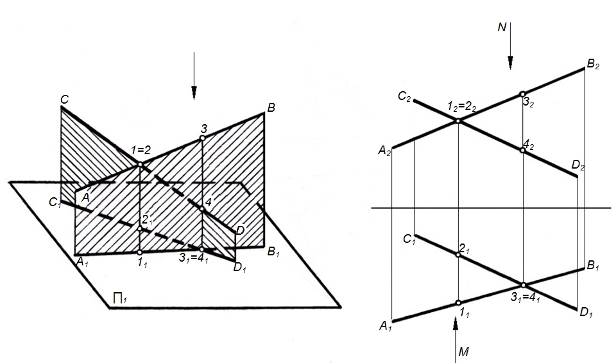
На рисунке 12а даны наглядные изображения двух скрещивающихся прямых АВ и СD, а также их комплексный чертеж (рисунок 12б). В пространстве такие прямые не имеют общих точек, на комплексном чертеже точки пересечения одноименных проекций скрещивающихся прямых не лежат на одной линии связи. Такие точки называются конкурирующими и используются для определения видимости чертежа.

а) б)

Рисунок 12 – Скрещивающиеся прямые

Важен вопрос, какая из прямых расположена выше и ближе к наблюдателю. На рисунке 12а (наглядное изображение) видно, что при взгляде сверху по указанной стрелке точка 3 на прямой АВ закрывает точку 4, а при взгляде спереди точка 1 закрывает точку 2. На комплексном чертеже этих прямых видно, что 32 выше чем 42 и при взгляде сверху по стрелке N при проецировании на П1 точка 3₁ закрывает точку 4₁. При взгляде спереди по стрелке M видно, что точка 1₁ прямой АВ находится ближе к наблюдателю чем точка 2₁. При проекции на П2 точка 1₂ прямой АВ закрывает точку 2₂ прямой СD. Следует отметить, что точки 1 и 2 называют фронтально-конкурирующие, а точки 3 и 4 – горизонтально-конкурирующие.